题目内容
8.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )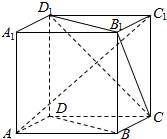
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |
分析 由BD∥B1D1,得到BD∥平面CB1D1;由AC⊥BD,CC1⊥BD,得到AC1⊥BD;异面直线AD与CB1角为45°;由AC1⊥B1D1,AC1⊥CB1,得到AC1⊥平面CB1D1.
解答  解:在A中,∵BD∥B1D1,BD?平面CB1D1,B1D1?平面CB1D1,
解:在A中,∵BD∥B1D1,BD?平面CB1D1,B1D1?平面CB1D1,
∴BD∥平面CB1D1,故A正确;
在B中,∵ABCD是正方形,∴AC⊥BD,
∵ABCD-A1B1C1D1为正方体,∴CC1⊥BD,
∵AC∩CC1=C,∴BD⊥平面ACC1,∴AC1⊥BD,故B正确;
在C中,∵AD∥BC,∴∠BCB1是异面直线AD与CB1所成角,
∵BCC1B1是正方形,∴∠BCB1=45°,
∴异面直线AD与CB1角为45°,故C错误;
在D中,∵A1B1C1D1是正方形,∴A1C1⊥B1D1,
∵ABCD-A1B1C1D1为正方体,∴CC1⊥B1D1,
∵A1C1∩CC1=C1,∴B1D1⊥平面ACC1,∴AC1⊥B1D1,
同理,AC1⊥CB1,∵B1D1∩CB1=B1,∴AC1⊥平面CB1D1,故D正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意正方体结构特征的合理运用.

练习册系列答案
相关题目
3.经过平面外一点与平面垂直的平面有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
20.已知P(xp,5)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)上的一点,F1,F2分别是双曲线的左,右焦点,若|PF1|•|PF2|=$\frac{9}{4}$ac,△PF1F2的内切圆的面积为4π,则双曲线Γ的渐近线方程为( )
| A. | y=$±\sqrt{2}$x | B. | y=±$\frac{\sqrt{7}}{3}$x | C. | y=±$\frac{4}{3}$x | D. | y=±$\sqrt{6}$x |
17.已知A={2,3,4},B={x||x|<3},则A∩B=( )
| A. | {3} | B. | {2,3} | C. | {2} | D. | {2,3,4} |
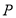 到点
到点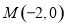 和到直线
和到直线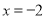 的距离相等,则动点
的距离相等,则动点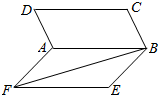 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.