题目内容
已知函数f(x)=sin(x-
)(x∈[0,2π)),若存在实数x1x2,满足f(x1)=f(x2)(x1≠x2),则x1+x2= .
| π |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:先求出函数在[0,2π)的对称轴,从而可求x1+x2的值.
解答:
解:∵f(x)=sin(x-
)(x∈[0,2π)),
∴令x-
=kπ+
,k∈Z可解得:x=kπ+
,k∈Z,k=0时,x=
,
故可得在[0,2π)上函数的对称轴是x=
,
∴若存在实数x1x2,满足f(x1)=f(x2)(x1≠x2),
则x1,x2,关于x=
对称,
∴x1+x2=
,
故答案为:
.
| π |
| 3 |
∴令x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| 5π |
| 6 |
故可得在[0,2π)上函数的对称轴是x=
| 5π |
| 6 |
∴若存在实数x1x2,满足f(x1)=f(x2)(x1≠x2),
则x1,x2,关于x=
| 5π |
| 6 |
∴x1+x2=
| 5π |
| 3 |
故答案为:
| 5π |
| 6 |
点评:本题考查正弦函数的图象,函数的零点的判定方法,体现了数形结合及转化的数学思想,属于基本知识的考查.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
将函数f(x)=sin2x的图象向右平移
个单位,得到函数y=g(x)的图象,则它的一个对称中心是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
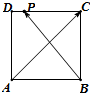 如图,正方形ABCD的边长为2,P是线段DC上的动点(含端点),则
如图,正方形ABCD的边长为2,P是线段DC上的动点(含端点),则