题目内容
已知点A(2,5),直线l:2x-3y-2=0,点M与点A关于l对称,
(1)求点M的坐标;
(2)若点B,C分别在直线l与y轴上运动,求△ABC周长的最小值.
(1)求点M的坐标;
(2)若点B,C分别在直线l与y轴上运动,求△ABC周长的最小值.
考点:与直线关于点、直线对称的直线方程,两点间的距离公式
专题:直线与圆
分析:(1)设点M的坐标为(a,b),由垂直平分可得
,解方程组可得;
(2)由(1)知点A关于l的对称点M(6,-1),又可得A关于y轴的对称点N(-2,5),由对称性可知△ABC周长的最小值即为MN的距离,由距离公式可得.
|
(2)由(1)知点A关于l的对称点M(6,-1),又可得A关于y轴的对称点N(-2,5),由对称性可知△ABC周长的最小值即为MN的距离,由距离公式可得.
解答:
解:(1)设点M的坐标为(a,b),
则
,
化简可得
,
解得
,即M坐标为(6,-1);
(2)由(1)知点A关于l的对称点M(6,-1),
又可得A关于y轴的对称点N(-2,5),
由对称性可知△ABC周长c=AB+BC+CA当M、B、C、N四点共线时取值最小值,
此时c=MB+BC+CN=MN=
=10
则
|
化简可得
|
解得
|
(2)由(1)知点A关于l的对称点M(6,-1),
又可得A关于y轴的对称点N(-2,5),
由对称性可知△ABC周长c=AB+BC+CA当M、B、C、N四点共线时取值最小值,
此时c=MB+BC+CN=MN=
| (-2-6)2+(5+1)2 |
点评:本题考查直线的对称性,涉及方程组的解法和垂直关系,属中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,输出的S是( )


| A、10 | B、15 | C、20 | D、35 |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
设函数f(x)=log2(x2-4x+a)(a>4),若所有点(s,f(t))(s,t∈[1,3])构成一个正方形区域,则函数f(x)的单调增区间为( )
| A、[1,2] |
| B、[2,3] |
| C、(-∞,2] |
| D、[2,+∞) |
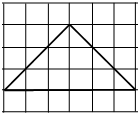
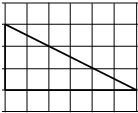
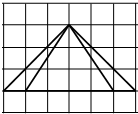
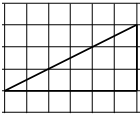
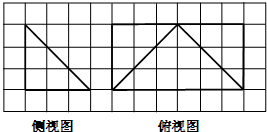 如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )
如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )