题目内容
将函数f(x)=sin2x的图象向右平移
个单位,得到函数y=g(x)的图象,则它的一个对称中心是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:将函数f(x)=sin2x的图象向右平移
个单位,得到解析式y=g(x)=sin2(x-
),令2(x-
)=kπ,k∈Z,可解得它的一个对称中心.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:∵将函数f(x)=sin2x的图象向右平移
个单位,得到函数y=g(x)=sin2(x-
)
∴令2(x-
)=kπ,k∈Z,可解得x=
+
,k∈Z,
当k=0时,有x=
,
故选:C.
| π |
| 6 |
| π |
| 6 |
∴令2(x-
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
当k=0时,有x=
| π |
| 6 |
故选:C.
点评:本题主要考查了函数y=Asin(ωx+φ)的图象变换,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
相关题目
设函数f(x)=log2(x2-4x+a)(a>4),若所有点(s,f(t))(s,t∈[1,3])构成一个正方形区域,则函数f(x)的单调增区间为( )
| A、[1,2] |
| B、[2,3] |
| C、(-∞,2] |
| D、[2,+∞) |
已知实数x,y满足
,若z=
的最大值为
,则a的值是( )
|
| ay |
| 3(x+1) |
| 1 |
| 8 |
| A、1 | ||
| B、-1 | ||
C、-
| ||
D、
|
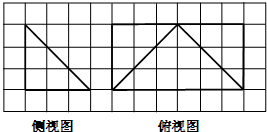 如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )
如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )