题目内容
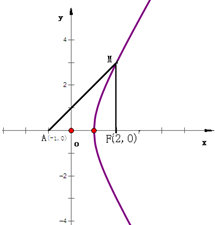 已知曲线C:x2-
已知曲线C:x2-| y2 |
| 3 |
(1)设M为曲线C上x轴上方任一点,求证:∠MFA=2∠MAF;
(2)若曲线C上存在两点C,D关于直线l:y=-
| 1 |
| 2 |
(3)在(2)的条件下,是否存在过C、A、D、F的圆,且该圆的半径为
| 3 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设M点坐标为(x0,y0),则y02=3(
-1).由于点M为x轴上方的一点,tan∠MAF=kMA,tan∠MFA=-kMF,由此由正切函数的性质,能证明∠MFA=2∠MAF.
(2)设直线CD的方程为y=2x+m,代入x2-
=1中,得x2+4mx+m2+3=0,由此利用根的判别式和韦达定理能求出b的取值范围.
(3)法一:假如四点C、A、D、F共圆,圆心恰在x轴上,所以AF为外接圆的直径,由双曲线的对称性,CD⊥AF,这与kCD=2不符,故假设错误,所以四点C、A、D、F不可能共圆于半径为
的圆.
(3)法二:假如四点C、A、D、F共圆,由圆的半径为
,得b=
,与(2)的结论b>4不符,故假设错误,所以四点C、A、D、F不可能共圆于半径为
的圆.
| x | 2 0 |
(2)设直线CD的方程为y=2x+m,代入x2-
| y2 |
| 3 |
(3)法一:假如四点C、A、D、F共圆,圆心恰在x轴上,所以AF为外接圆的直径,由双曲线的对称性,CD⊥AF,这与kCD=2不符,故假设错误,所以四点C、A、D、F不可能共圆于半径为
| 3 |
| 2 |
(3)法二:假如四点C、A、D、F共圆,由圆的半径为
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
解答:
(1)证明:设M点坐标为(x0,y0),则有x02-
=1,即y02=3(
-1).
由于点M为x轴上方的一点,tan∠MAF=kMA,
tan∠MFA=-kMF=
tan2∠MAF=
=
=
=
=
=
=
,
又∠MFA、2∠MAF∈(0,π),且由正切函数的性质,有∠MFA=2∠MAF,
∴∠MFA=2∠MAF.…(5分)
(2)解:设直线CD的方程为y=2x+m,代入x2-
=1中,
得x2+4mx+m2+3=0,(1)
由于方程(1)有两不等正根,
设C、D的坐标分别为(x1,y1),(x2,y2),
则有
,解得m<-1,
又∵线段CD的中点M(-2m,-3m)也在直线y=-
x+b上,
于是有-3m=m+b,b=-4m,∴b>4.…(10分)
(3)解法一:假如四点C、A、D、F共圆,
则圆心在直线x=
及直线y=-
x+b上,圆心坐标为(
,b-
),
又由于圆的半径为
,由
=
,得b=
,
从而圆心恰在x轴上,所以AF为外接圆的直径,
∴∠ACF=90°,又由∠CFA=2∠CAF知
,同理∠DAF=30°,
由双曲线的对称性,CD⊥AF,这与kCD=2不符,故假设错误,
∴四点C、A、D、F不可能共圆于半径为
的圆.…(14分)
(3)解法二:假如四点C、A、D、F共圆,
则圆心在直线x=
及直线y=-
x+b上,圆心坐标为(
,b-
),
又由于圆的半径为
,由
=
,得b=
,
与(2)的结论b>4不符,故假设错误,
∴四点C、A、D、F不可能共圆于半径为
的圆.…(14分)
| ||
| 3 |
| x | 2 0 |
由于点M为x轴上方的一点,tan∠MAF=kMA,
tan∠MFA=-kMF=
| y0 |
| 2-x0 |
| 2tan∠MAF |
| 1-tan2∠MAF |
| 2kMA |
| 1-kMA2 |
=
2
| ||
1-(
|
| 2(x0+1)y0 |
| (x0+1)2-y02 |
=
| 2(x0+1)y0 |
| (x0+1)2-3(x02-1) |
| 2y0 |
| 4-2x0 |
| y0 |
| 2-x0 |
又∠MFA、2∠MAF∈(0,π),且由正切函数的性质,有∠MFA=2∠MAF,
∴∠MFA=2∠MAF.…(5分)
(2)解:设直线CD的方程为y=2x+m,代入x2-
| y2 |
| 3 |
得x2+4mx+m2+3=0,(1)
由于方程(1)有两不等正根,
设C、D的坐标分别为(x1,y1),(x2,y2),
则有
|
又∵线段CD的中点M(-2m,-3m)也在直线y=-
| 1 |
| 2 |
于是有-3m=m+b,b=-4m,∴b>4.…(10分)
(3)解法一:假如四点C、A、D、F共圆,
则圆心在直线x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又由于圆的半径为
| 3 |
| 2 |
(
|
| 3 |
| 2 |
| 1 |
| 4 |
从而圆心恰在x轴上,所以AF为外接圆的直径,
∴∠ACF=90°,又由∠CFA=2∠CAF知
|
由双曲线的对称性,CD⊥AF,这与kCD=2不符,故假设错误,
∴四点C、A、D、F不可能共圆于半径为
| 3 |
| 2 |
(3)解法二:假如四点C、A、D、F共圆,
则圆心在直线x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又由于圆的半径为
| 3 |
| 2 |
(
|
| 3 |
| 2 |
| 1 |
| 4 |
与(2)的结论b>4不符,故假设错误,
∴四点C、A、D、F不可能共圆于半径为
| 3 |
| 2 |
点评:本题考查两角相等的证明,考查实数的取值范围的求法,考查四点共圆的判断与求法,解题时要认真审题,注意反证法的合理运用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
