题目内容
△ABC的三个内角A、B、C所对的边分别是a,b,c;asinAsinB+bcos2A=
a
(1)求
;
(2)若c=
,b=
,求cosB的值.
| 2 |
(1)求
| b |
| a |
(2)若c=
| 3 |
| 2 |
考点:正弦定理,余弦定理
专题:计算题,三角函数的求值
分析:(1)利用正弦定理化边为角可求
=
,从而可得答案;
(2)由(1)易求a,再用余弦定理可求;
| sinB |
| sinA |
| 2 |
(2)由(1)易求a,再用余弦定理可求;
解答:
解:(1)asinAsinB+bcos2A=
a,
由正弦定理可得,sin2AsinB+sinBbcos2A=
sinA,即即sinB=
sinA,
∴
=
,则
=
;
(2)由(1)知
=
,即
=
,
∴a=1,
∴cosB=
=
=
.
| 2 |
由正弦定理可得,sin2AsinB+sinBbcos2A=
| 2 |
| 2 |
∴
| sinB |
| sinA |
| 2 |
| b |
| a |
| 2 |
(2)由(1)知
| b |
| a |
| 2 |
| ||
| a |
| 2 |
∴a=1,
∴cosB=
| a2+c2-b2 |
| 2ac |
| 1+3-2 | ||
2
|
| ||
| 3 |
点评:该题考查正弦定理、余弦定理及其应用,熟记相关公式并能灵活运用是解题关键.

练习册系列答案
相关题目
执行如图所示的程序框图,输入m=39,n=27,则输出的实数m的值是( )


| A、27 | B、12 | C、9 | D、3 |
函数y=sin2x-4sinx+5的值域为( )
| A、[1,+∞] |
| B、(1,+∞) |
| C、[2,10] |
| D、[1,10] |
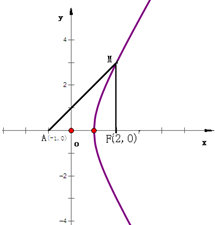 已知曲线C:x2-
已知曲线C:x2-