Question

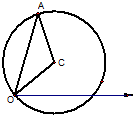已知在一个极坐标系中点C的极坐标为(2，

π

3

)．
（1）求出以C为圆心，半径长为2的圆的极坐标方程（写出解题过程）并画出图形
（2）在直角坐标系中，以圆C所在极坐标系的极点为原点，极轴为x轴的正半轴建立直角坐标系，点P是圆C上任意一点，Q(5，-

3

)，M是线段PQ的中点，当点P在圆C上运动时，求点M的轨迹的普通方程．

Answer 1

考点：简单曲线的极坐标方程

专题：坐标系和参数方程

分析：（1）如图，设圆C上任意一点A(ρ，θ)，则∠AOC=θ-

π

3

或

π

3

-θ．由余弦定理得：4+ρ2-4cos(θ-

π

3

)=4，化简即可得出．
（2）利用圆的方程、中点坐标公式可得点M的参数方程

x= 6+2cosα 2 y= 2sinα 2

，消去参数即可得到普通方程．

解答： 解：（1）如图，设圆C上任意一点A(ρ，θ)，则∠AOC=θ-

π

3

或

π

3

-θ．
由余弦定理得：4+ρ2-4cos(θ-

π

3

)=4，
∴圆C的极坐标方程ρ=4cos(θ-

π

3

)．
（2）在直角坐标系中，点C的坐标为(1，

3

)，可设圆C上任意一点P(1+2cosα，

3

+2sinα)
又令M（x，y）由Q(5，-

3

)，M是线段PQ的中点．
∴M的参数方程为：

x= 6+2cosα 2 y= 2sinα 2

⇒

x=3+cosα y=sinα

(α为参数)．
∴点M的轨迹的普通方程为：（x-3）²+y²=1．

点评：本题考查了极坐标方程与直角坐标方程的互化、参数方程化为普通方程、中点坐标方程、余弦定理，考查了推理能力与计算能力，属于中档题．