题目内容
若将函数y=sin(2x-
)的图象向左平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦、余弦函数的图象的对称性,可得φ的最小正值.
解答:
解:将函数y=sin(2x-
)的图象向左平移φ个单位,所得图象对应的函数解析式为 函数y=sin(2x+2φ-
),
根据所得图象关于y轴对称,可得2φ-
=kπ+
,k∈z,即 φ=
kπ+
,则φ的最小正值为
,
故选:C.
| π |
| 4 |
| π |
| 4 |
根据所得图象关于y轴对称,可得2φ-
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 3π |
| 8 |
| 3π |
| 8 |
故选:C.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦、余弦函数的图象的对称性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知曲线y=
在点M(π,0)处的切线为l,若θ为l的倾斜角,则点P(sinθ,cosθ)在( )
| sinx |
| x |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
在矩形ABCD中,O是矩形对角线的交点,
,
是平面上不共线的向量,若
=5
,
=3
,则
=( )
| e1 |
| e2 |
| BC |
| e1 |
| DC |
| e2 |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=ax+1-3(a为常数),则f(-1)的值为( )
| A、-6 | B、-3 | C、-2 | D、6 |
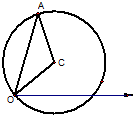 已知在一个极坐标系中点C的极坐标为
已知在一个极坐标系中点C的极坐标为