题目内容
3．将一颗骰子连续抛掷2次，则向上的点数之和为8的概率为（ ）| A． | $\frac{1}{9}$ | B． | $\frac{5}{36}$ | C． | $\frac{3}{18}$ | D． | $\frac{1}{72}$ |
分析 先求出基本事件总数，再求出向上的点数之和为8包含的基本事件个数，由此能求出向上的点数之和为8的概率．
解答 解：将一颗骰子连续抛掷2次，
基本事件总数n=6×6=36，
向上的点数之和为8包含的基本事件有：
（2，6），（6，2），（3，5），（5，3），（4，4），共5个，
∴向上的点数之和为8的概率为p=$\frac{5}{36}$．
故选：B．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
13．如果实数x，y满足（x-2）2+y2=2，则$\frac{y}{x}$的范围是（ ）
| A． | （-1，1） | B． | [-1，1] | C． | （-∞，-1）∪（1，+∞） | D． | （-∞，-1]∪[1，+∞） |
14．不等式2x2-x＞0的解集是（ ）
| A． | （-∞，0）∪（$\frac{1}{2}$，+∞） | B． | （-∞，$\frac{1}{2}$） | C． | （0，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，+∞） |
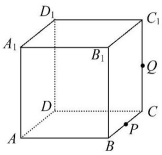如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是①②④（写出所有正确命题的编号）．
8．在△ABC中，若b=3，A=120°，三角形的面积$S=\frac{9}{4}\sqrt{3}$，则三角形外接圆的半径为（ ）
| A． | $\frac{2}{3}\sqrt{3}$ | B． | 3 | C． | $\frac{4}{3}\sqrt{3}$ | D． | 6 |