题目内容
15.某校共有高一、高二、高三学生1290人,其中高一480人,高二比高三多30人,为了解该校学生的身体健康情况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生96人,则该样本中的高二学生人数为( )| A. | 84 | B. | 78 | C. | 81 | D. | 96 |
分析 根据分层抽样的定义建立比例关系即可.
解答 解:∵高一480人,高二比高三多30人,
∴设高三x人,则x+x+30+480=1290,
解得x=390,
故高二420,高三390人,
若在抽取的样本中有高一学生96人,
则该样本中的高三学生人数为$\frac{96}{480}$=78.
故选:B
点评 本题主要考查分层抽样的应用,根据比例关系是解决本题的关键.

练习册系列答案
相关题目
3.将一颗骰子连续抛掷2次,则向上的点数之和为8的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{5}{36}$ | C. | $\frac{3}{18}$ | D. | $\frac{1}{72}$ |
10.若函数$f(x)={x^2}+ax+\frac{1}{x}$在$({\frac{1}{2}\;\;,\;\;1})$内任取两个实数p,q,且p≠q,不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,则a的取值范围是( )
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
7.已知双曲线$\frac{y^2}{4}-{x^2}=1$的两条渐近线分别与抛物线y2=2px(p>0)的准线交于A,B两点,O为坐标原点,若△OAB的面积为1,则p的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 4 |
4.复数$z=2i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.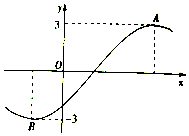 已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )