题目内容
4.已知等差数列{an}中,公差d≠0,a4=10,且a3,a6,a10成等比数列,则数列{an}前9项的和为( )| A. | 99 | B. | 90 | C. | 84 | D. | 70 |
分析 运用等比数列的中项的性质和等差数列的通项公式,可得d的方程,解方程可得d,求出通项公式,由等差数列求和公式计算即可得到所求和.
解答 解:∵{an}为等差数列,且公差为d≠0,
∴a3=a4-d=10-d,
∴a6=a4+2d=10+2d,
a10=a4+6d=10+6d,
∵a3,a6,a10成等比数列
即(10-d)(10+6d)=(10+2d)2,
整理得10d2-10d=0,
解得d=1或d=0(舍去).
∴数列{an}的通项公式为an=n+6.
则数列{an}前9项的和为$\frac{1}{2}$(a1+a9)×9=$\frac{1}{2}$×(7+15)×9=99.
故选:A.
点评 本题考查等差数列的通项公式和求和公式的运用,等比数列的中项的性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
12.某大学有甲、乙两个图书馆,对其借书的等待时间进行调查,得到下表:
甲图书馆
乙图书馆
(1)分别求在甲、乙两图书馆借书的平均等待时间;
(2)以表中等待时间的学生人数的频率为概率,若某同学希望借书等待时间不超过3分钟,请问在哪个图书馆借更能满足他的要求?
甲图书馆
| 借书等待时间T1(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1500 | 1000 | 500 | 500 | 1500 |
| 借书等待时间T2(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1000 | 500 | 2000 | 1250 | 250 |
(2)以表中等待时间的学生人数的频率为概率,若某同学希望借书等待时间不超过3分钟,请问在哪个图书馆借更能满足他的要求?
9.已知函数f(x)在定义域R上的导函数为f′(x),若方程f'(x)=0无解,且f[f(x)-2017x]=2017,当g(x)=sinx-cosx-kx在[-$\frac{π}{2}$,$\frac{π}{2}$]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
9.已知α为第二象限角.且sin2α=-$\frac{24}{25}$,则cosα-sinα的值为( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
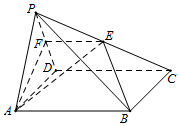 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F