题目内容
19.已知函数f(x)=x-a-lnx(a∈R).(1)若f(x)≥0恒成立,求实数a的取值范围;
(2)证明:若0<x1<x2,则x1lnx1-x1lnx2>x1-x2.
分析 (1)判断f(x)的单调性,计算f(x)的最小值,令fmin(x)≥0即可得出a的范围;
(2)令a=1,根据f(x)≥0得出lnx≤x-1在(0,+∞)上恒成立,把x=$\frac{{x}_{2}}{{x}_{1}}$代入化简即可得出结论.
解答 解:(1)f(x)的定义域为(0,+∞),
f(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
令f'(x)>0,得x>1;令f'(x)<0,得0<x<1,
∴f(x)在(0,1)单调递减,在(1,+∞)上单调递增,
∴fmin(x)=f(1)=1-a,
∵f(x)≥0恒成立,
∴1-a≥0,解得a≤1.
(2)证明:取a=1,f(x)=x-1-lnx,
由(1)知x-1-lnx≥0恒成立,即lnx≤x-1恒成立,
∴$ln\frac{x_2}{x_1}<\frac{x_2}{x_1}-1$,(0<x1<x2),
∴lnx2-lnx1<$\frac{{x}_{2}}{{x}_{1}}$-1,∴x1lnx2-x1lnx1<x2-x1.
∴x1lnx1-x1lnx2>x1-x2.
点评 本题考查了导数与函数单调性的关系,函数最值的计算及单调性应用,属于中档题.

练习册系列答案
相关题目
9.已知α为第二象限角.且sin2α=-$\frac{24}{25}$,则cosα-sinα的值为( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
10.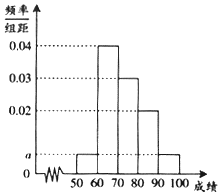 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)
 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x::y | 1:1 | 2:1 | 3:4 | 4:5 |
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)
9.设a、b、c是正实数,则“a、b、c依次成等差数列”是“$b≥\sqrt{ac}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |