题目内容
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=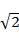 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
(1)求直线PB与平面POC所成角的余弦值;
(2)求B点到平面PCD的距离;
(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为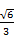 ?若存在,求出
?若存在,求出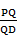 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

[解析](1)在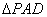 中,
中, 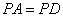 ,
,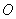 为
为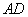 中点,所以
中点,所以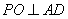 ,又侧面
,又侧面 底面
底面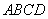 ,平面
,平面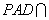 平面
平面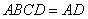 ,
,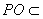 平面
平面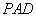 ,所以
,所以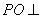 平面
平面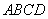 .
.
又在直角梯形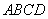 中,连结
中,连结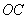 ,易得
,易得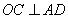 ,所以以
,所以以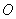 为坐标原点,直线
为坐标原点,直线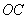 为
为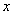 轴,直线
轴,直线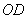 为
为 轴,直线
轴,直线 为
为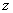 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
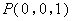 ,
,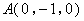 ,
,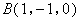 ,
,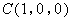 ,
,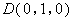
∴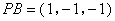 ,易证
,易证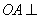 平面
平面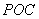 ,
,
∴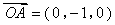 是平面
是平面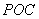 的法向量,
的法向量,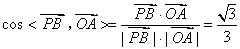 .
.
∴直线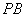 与平面
与平面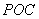 所成角的余弦值为
所成角的余弦值为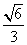 .
.
(2)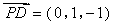 ,
,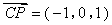
设平面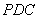 的一个法向量为
的一个法向量为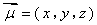 ,
,
则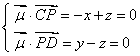 ,取
,取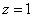 ,得
,得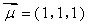 .
.
∴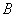 点到平面
点到平面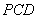 的距离
的距离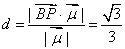 .
.
(3)存在.设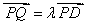 (
(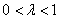 ),
),
∵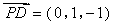 ,∴
,∴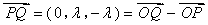 ,
,
∴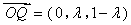 ,∴
,∴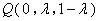 .
.
设平面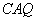 的一个法向量为
的一个法向量为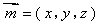 ,
,
则 ,取
,取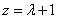 ,得
,得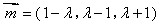 .
.
又平面 的一个法向量为
的一个法向量为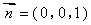 ,
,
∵二面角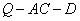 的余弦值为
的余弦值为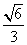 ,∴
,∴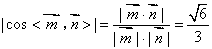 ,
,
得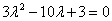 ,解得
,解得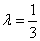 或
或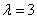 (舍),
(舍),
∴存在点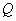 ,使得二面角
,使得二面角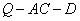 的余弦值为
的余弦值为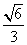 ,且
,且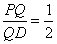 .
.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
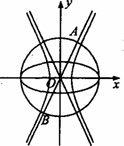
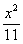 +y2=1,双曲线C2:
+y2=1,双曲线C2: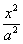 —
—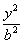 =1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( )
=1(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A、B两点,且C1与该渐近线的两交点将线段AB三等分,则C2的离心率为 ( ) B.5 C.
B.5 C.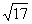 D.
D.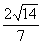
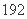 种 B.
种 B. 种 C.
种 C.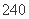 种 D.
种 D. 种
种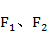 ,点A在C上.若|
,点A在C上.若|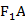 |=2|
|=2| |,则cos∠
|,则cos∠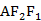 =( )
=( ) B.
B. C.
C.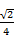 D.
D.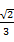
 的参数方程是
的参数方程是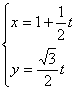 (
(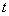 为参数),以原点
为参数),以原点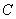 的极坐标方程为
的极坐标方程为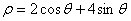 ,则直线
,则直线 则y-4x的最大值是( )
则y-4x的最大值是( ) C.4 D.7
C.4 D.7 B.81
B.81  是等差数列
是等差数列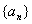 的前n项和,若
的前n项和,若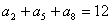 , 则
, 则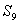 等于( )
等于( )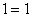 第一个式子
第一个式子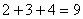 第二个式子
第二个式子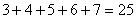 第三个式子
第三个式子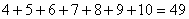 第四个式子
第四个式子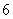 个等式;
个等式;