题目内容
(1)已知集合A={a2,a+1,-3},B={a-3,2a-1,a2+1},若A∩B={-3},求实数a的值
(2)已知集合A={x|x2-5x-6=0},集合B={x|mx+1=0}若A∪B=A,求实数m组成的集合.
(2)已知集合A={x|x2-5x-6=0},集合B={x|mx+1=0}若A∪B=A,求实数m组成的集合.
考点:子集与交集、并集运算的转换
专题:计算题
分析:(1)根据A∩B={-3},得到-3∈B,然后根据元素和集合关系,解实数a即可.
(2)先求得A,再根据A∪B=A,可得B⊆A,分B=∅和B≠∅两种情况,分别求得m的值,可得实数m组成的集合.
(2)先求得A,再根据A∪B=A,可得B⊆A,分B=∅和B≠∅两种情况,分别求得m的值,可得实数m组成的集合.
解答:
(1)∵A∩B={-3},∴-3∈B,而a2+1≠-3,
∴当a-3=-3,a=0,A={0,1,-3},B={-3,-1,1},
这样A∩B={-3,1}与A∩B={-3}矛盾;
当2a-1=-3,a=-1,符合A∩B={-3}
∴a=-1
(2)由于集合A={x|x2-5x-6=(x+1)(x-6)=0}={-1,6},集合B={x|mx+1=0},且A∪B=A,∴B⊆A.
当B=∅时,m=0;
当B≠∅时,由于B={
},∴
=-1,或
=6,解得m=1,或m=-
.
故实数m组成的集合为(0,1,-
}.
∴当a-3=-3,a=0,A={0,1,-3},B={-3,-1,1},
这样A∩B={-3,1}与A∩B={-3}矛盾;
当2a-1=-3,a=-1,符合A∩B={-3}
∴a=-1
(2)由于集合A={x|x2-5x-6=(x+1)(x-6)=0}={-1,6},集合B={x|mx+1=0},且A∪B=A,∴B⊆A.
当B=∅时,m=0;
当B≠∅时,由于B={
| 1 |
| -m |
| 1 |
| -m |
| 1 |
| -m |
| 1 |
| 6 |
故实数m组成的集合为(0,1,-
| 1 |
| 6 |
点评:本题主要考查集合中参数的取值范围问题,集合间的包含关系,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
设函数f(x)=-x+2,x∈[-5,5],若从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A、0.5 | B、0.4 |
| C、0.3 | D、0.2 |
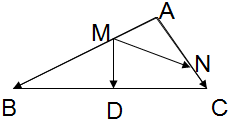 如图:在△ABC中,D为BC中点,AM=
如图:在△ABC中,D为BC中点,AM=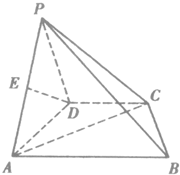 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD与底面ABCD垂直,E为PA的中点.