题目内容
6．5个人分4张无座足球票，每人至多分一张，而且必须分完，不同的分发种数有（ ）| A． | $A_5^4$种 | B． | 45种 | C． | $C_5^4$种 | D． | 54种 |
分析 由题意知5个人分4张同样的足球票，每人至多分1张，而且票必须分完，则满足条件的分法是只有一个人没有票，共有五种结果．
解答 解：由题意知5个人分4张同样的足球票，每人至多分1张，而且票必须分完，
则满足条件的分法是只有一个人没有票，
∴不同的分发种数有${C}_{5}^{4}$种，
故选：C．
点评 这是一个简单计数问题，实际上本题也可以按照平均分组来理解，即把第一张票有五种方法，第二张票有4种方法，第三张票有3种方法，第四张票有2种方法，因为四张票相同，故排列以后再除以A44．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
2．函数f（x）=x（1+$\sqrt{1-{x}^{2}}$）的最大值是（ ）
| A． | 3$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | $\frac{3\sqrt{3}}{4}$ |
14．函数f（x）=$\frac{{\root{3}{x^2}}}{e^x}$在x∈[-2，2]上的极值点的位置有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
1．用数学归纳法证明$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…$\frac{1}{2n}$＜1（n∈N*且n＞1）由n=k到n=k+1时，不等式左边应添加的项是（ ）
| A． | $\frac{1}{2（k+1）}$ | B． | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k}$ | ||
| C． | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$ | D． | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$-$\frac{1}{k+2}$ |
15．某公司在一次对员工的休闲方式（看电视与运动）与性别之间是否有关系的调查中，共调查了124人，其中女性70人中主要休闲方式是看电视的有43人，男性中主要休闲方式是运动的有33人．
（1）根据以上数据建立一个2×2的列联表；
（2）检验性别与休闲方式是否有关系．
${Χ^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
（1）根据以上数据建立一个2×2的列联表；
（2）检验性别与休闲方式是否有关系．
${Χ^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P（Χ2≥k） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
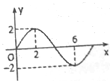函数f（x）=Asinωx（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（2017）=$\sqrt{2}$．