题目内容
已知f（x）=x5+ax7+bx15+cx23+ex-10且f（-2）=36，那么f（2）= ．
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：计算f（-x），运用奇函数的定义，即可得到f（-x）+f（x）=-20，由f（-2），即可得到f（2）．
解答：
解：由f（x）=x5+ax7+bx15+cx23+ex-10，
则f（-x）=（-x）5+ax7+b（-x）15+c（-x）23+e（-x）-10
=-（x5+ax7+bx15+cx23+ex）-10，
则f（-x）+f（x）=-20，
即有f（2）=-20-f（-2）=-20-36=-56．
故答案为：-56．
则f（-x）=（-x）5+ax7+b（-x）15+c（-x）23+e（-x）-10
=-（x5+ax7+bx15+cx23+ex）-10，
则f（-x）+f（x）=-20，
即有f（2）=-20-f（-2）=-20-36=-56．
故答案为：-56．
点评：本题考查函数的奇偶性的运用：求函数值，考查运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知某几何体的三视图如上图所示（单位：cm），则该几何体的表面积是（ ）
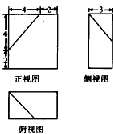
A、（124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |
