题目内容
直线:ax-y-(a-5)=0(a是参数)与抛物线f:y=(x+1)2的相交弦是AB,求弦AB的中点轨迹方程.(利用点差法)
考点:轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:a≠0时,设A(x1,y1),B(x2,y2),设中点C(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)分别代入y=(x+1)2,利用点差法能求出弦AB的中点轨迹方程.
解答:
解:联立
,
化解得到x2+(2-a)x+a+6=0,
a=0时,(x+1)2=-5,不成立,方程组无解,即直线与抛物线不相交;
a≠0时,设A(x1,y1),B(x2,y2),
设中点C(x,y),则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入y=(x+1)2,
得
,两式相减得y1-y2=(x1+x2)(x1-x2)+2(x1-x2),
∴y1-y2=(2x+2)(x1-x2),
∴k=
=2x+2,
∵直线ax-y-(a-5)=0过点(0,5-a),(x,y),
∴k=
,
∴
=2x+2,
整理,得2x2+2x-y-a+5=0.
∴弦AB的中点轨迹方程为2x2+2x-y-a+5=0.
|
化解得到x2+(2-a)x+a+6=0,
a=0时,(x+1)2=-5,不成立,方程组无解,即直线与抛物线不相交;
a≠0时,设A(x1,y1),B(x2,y2),
设中点C(x,y),则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入y=(x+1)2,
得
|
∴y1-y2=(2x+2)(x1-x2),
∴k=
| y1-y2 |
| x1-x2 |
∵直线ax-y-(a-5)=0过点(0,5-a),(x,y),
∴k=
| y-5+a |
| x |
∴
| y-5+a |
| x |
整理,得2x2+2x-y-a+5=0.
∴弦AB的中点轨迹方程为2x2+2x-y-a+5=0.
点评:本题考查弦中点的轨迹方程的求法,是中档题,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
已知抛物线y2=2px(p>0)与双曲线
-
=1(a>0,b>0)有共同的焦点F,P为抛物线与双曲线的一个交点,且∠PFO=
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
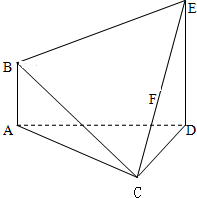 如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.
如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.