题目内容
已知抛物线y2=2px(p>0)与双曲线
-
=1(a>0,b>0)有共同的焦点F,P为抛物线与双曲线的一个交点,且∠PFO=
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:抛物线的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:F(
,0),
=c.由∠PFO=
,可得kPF=tan
=-
,直线PF的方程为:y=-
(x-
).与抛物线方程联立可得12x2-20px+3p2=0,解得x=
,代入y2=2px,可得P(
,
p)即P(
c,
c).代入双曲线方程可得:
-
=1,又b2=c2-a2,解出即可.
| p |
| 2 |
| p |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 3 |
| 3 |
| p |
| 2 |
| p |
| 6 |
| p |
| 6 |
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| c2 |
| 9a2 |
| 4c2 |
| 3b2 |
解答:
解:F(
,0),
=c.
∵∠PFO=
,∴kPF=tan
=-
,
∴直线PF的方程为:y=-
(x-
).
联立
,化为12x2-20px+3p2=0,
解得x=
,或
p(舍去).
代入y2=2px,取y=
p,
∴P(
,
p)即P(
c,
c).
代入双曲线方程可得:
-
=1,又b2=c2-a2,
化为e4-22e2+9=0,
解得e2=11+2
,
∴e=2+
.
故选:B.
| p |
| 2 |
| p |
| 2 |
∵∠PFO=
| π |
| 3 |
| 2π |
| 3 |
| 3 |
∴直线PF的方程为:y=-
| 3 |
| p |
| 2 |
联立
|
解得x=
| p |
| 6 |
| 3 |
| 2 |
代入y2=2px,取y=
| ||
| 3 |
∴P(
| p |
| 6 |
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
代入双曲线方程可得:
| c2 |
| 9a2 |
| 4c2 |
| 3b2 |
化为e4-22e2+9=0,
解得e2=11+2
| 28 |
∴e=2+
| 7 |
故选:B.
点评:本题考查了抛物线与双曲线的标准方程及其性质、直线与抛物线相交问题转化为方程联立解出坐标,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下面的式子中成立的是( )
| A、0={x|x2=0} |
| B、∅?{x|x2+1=0,x∈R} |
| C、5∈{x|x=3k-1,k∈Z} |
| D、{0}∈N |
在直角坐标系中,过点A(0,3),B(
,0)的直线l的倾斜角是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)•g(y),③h(x•y)=h(x)+h(y),④m(x•y)=m(x)•m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )
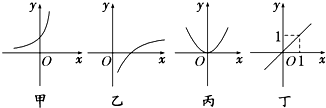

| A、①甲,②乙,③丙,④丁 |
| B、①乙,②丙,③甲,④丁 |
| C、①丙,②甲,③乙,④丁 |
| D、①丁,②甲,③乙,④丙 |