题目内容
19.已知ω>0,设x1,x2是方程sin(ωx+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$的两个不同的实数根,且|x2-x1|的最小值为2,则ω等于( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 由题意,ωx+$\frac{π}{3}$=$\frac{π}{3}$+2kπ或ωx+$\frac{π}{3}$=$\frac{2π}{3}$+2k′π,利用|x2-x1|的最小值为2,可得2ω=$\frac{π}{3}$,即可得出结论.
解答 解:∵sin(ωx+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
∴ωx+$\frac{π}{3}$=$\frac{π}{3}$+2kπ或ωx+$\frac{π}{3}$=$\frac{2π}{3}$+2k′π,
∵|x2-x1|的最小值为2,
∴2ω=$\frac{π}{3}$,∴ω=$\frac{π}{6}$,
故选:D.
点评 本题考查正弦函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.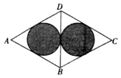 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )| A. | $\frac{\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{18π}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | $\frac{\sqrt{3}π}{9}$ |
10.若x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≤0\\ y≥0\end{array}\right.$,则x+2y的最大值为( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
7.某市小型机动车驾照“科二”考试共有五项考察项目,假设某人目前只训练了其中三个项目,现驾校欲从五项考察项目中任意抽出两项对其进行一次测试,则恰好抽到一项该人训练了的项目的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |