题目内容
9．
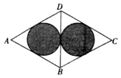如图所示，已知菱形ABCD是由等边△ABD与等边△BCD拼接而成，两个小圆与△ABD以及△BCD分别相切，则往菱形ABCD内投掷一个点，该点落在阴影部分内的概率为（ ）| A． | $\frac{\sqrt{3}}{9π}$ | B． | $\frac{\sqrt{3}}{18π}$ | C． | $\frac{\sqrt{3}π}{18}$ | D． | $\frac{\sqrt{3}π}{9}$ |
分析 设等边三角形的边长为a，则内切圆的半径为$\frac{\sqrt{3}}{6}$a，求出相应的面积，以面积为测度可得结论．
解答 解：设等边三角形的边长为a，则内切圆的半径为$\frac{\sqrt{3}}{6}$a，
∴往菱形ABCD内投掷一个点，该点落在阴影部分内的概率为$\frac{2×π×（\frac{\sqrt{3}}{6}a）^{2}}{2×\frac{\sqrt{3}}{4}{a}^{2}}$=$\frac{\sqrt{3}π}{9}$，
故选：D．
点评 本题考查几何概型，考查面积的计算，属于中档题．
练习册系列答案
相关题目
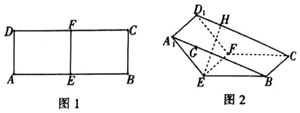如图1，在矩形ABCD中，AB=8，AD=3，点E，F分别为AB、CD的中点，将四边形AEFD沿EF折到A1EFD1的位置，使∠A1EB=120°，如图2所示，点G、H分别在A1B、D1C上，A1G=D1H=$\sqrt{3}$，过点G、H的平面α与几何体A1EB-D1FC的面相交，交线围成一个正方形．
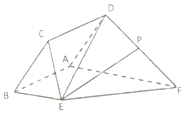如图，已知菱形ABCD与直角梯形ABEF所在的平面互相垂直，其中BE∥AF，∠EBA=90°，AB=BE=$\frac{1}{2}$AF=2，∠CBA=$\frac{π}{3}$，P为DF的中点．
19．已知ω＞0，设x1，x2是方程sin（ωx+$\frac{π}{3}$）=$\frac{\sqrt{3}}{2}$的两个不同的实数根，且|x2-x1|的最小值为2，则ω等于（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |