题目内容
11.已知实数x,y满足$\left\{\begin{array}{l}{y≤x-1}\\{x≤3}\\{x+y≥2}\end{array}\right.$,则$\frac{y}{x}$的取值范围是[$-\frac{1}{3}$,$\frac{2}{3}$].分析 由约束条件作出可行域,再由$\frac{y}{x}$的几何意义,即可行域内的动点与定点O(0,0)连线的斜率求解.
解答 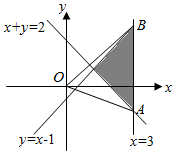 解:由约束条件$\left\{\begin{array}{l}{y≤x-1}\\{x≤3}\\{x+y≥2}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{y≤x-1}\\{x≤3}\\{x+y≥2}\end{array}\right.$作出可行域如图,
$\frac{y}{x}$的几何意义为可行域内的动点与定点O(0,0)连线的斜率,
联立方程组求得A(3,-1),B(3,2),
又${k}_{OA}=-\frac{1}{3}$,${k}_{OB}=\frac{2}{3}$.
∴$\frac{y}{x}$的取值范围是[$-\frac{1}{3}$,$\frac{2}{3}$].
故答案为:[$-\frac{1}{3}$,$\frac{2}{3}$].
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知ω>0,设x1,x2是方程sin(ωx+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$的两个不同的实数根,且|x2-x1|的最小值为2,则ω等于( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
6.为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房心理预测调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表:
已知样本中城市人数与农村人数之比是3:8.
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)从参与调研的城市人中用分层抽样方法抽取6人,进一步统计城市人的某项收入指标,假设一个买房人的指标算作3,一个纠结人的指标算作2,一个不买房人的指标算作1,现在从这6人中再随机选取3人,令X=再抽取3人指标之和,求X的分布列和数学期望.
3.某机械厂组装A,B两种类型机械,每组装1台A或B所需要的配件材料费和工人数如下表所示.
已知该机械厂现有工人32人,可用资金55万元,组装1台A类型机械可获纯利润4万元,组装1台B类型机械可获纯利润2万元,设该机械厂计划组装A,B两种类型机械分别为x台,y台.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问该机械厂分别组装A,B两种类型机械各多少台,才能获得最大利润?并求出此最大纯利润.
| 类型 条件 | A | B |
| 配件材料费(万元) | 20 | 5 |
| 工人数(人) | 4 | 8 |
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问该机械厂分别组装A,B两种类型机械各多少台,才能获得最大利润?并求出此最大纯利润.
9.在△ABC中,a,b,c分别是角A,B,C的对边,若(b-$\frac{6}{5}$c)sinB+csinC=asinA,则sinA=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
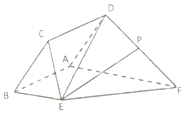 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,∠EBA=90°,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,∠EBA=90°,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.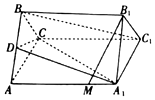 如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.
如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.