题目内容
求函数f（x）=
+
+
+
+
+
的最大值．
| 1+sinx |
| 1-sinx |
| 2+sinx |
| 2-sinx |
| 3+sinx |
| 3-sinx |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：首先利用技巧，巧设坐标，进一步利用基本不等式求解．
解答：
解：设：
a1=(
，
）
a2=(
，
)
a3=(
，
)
a4=(
，
)
a5=(
，
)
a5=(
，
)
a1+a2+a3+a4+a5+a6=（f（x），f（x））
|a1+a2+a3+a4+a5+a6|=
(f(x)
|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=2(
+2+
)≥f(x)
所以：f(x)≤2(1+
+
)
当且仅当：
=
=
=
=
=
即sinx=0，即x=kπ时，函数f(x)≤2(1+
+
)
a1=(
| 1+sinx |
| 1-sinx |
a2=(
| 1-sinx |
| 1+sinx |
a3=(
| 2+sinx |
| 2-sinx |
a4=(
| 2-sinx |
| 2+sinx |
a5=(
| 3+sinx |
| 3-sinx |
a5=(
| 3-sinx |
| 3+sinx |
a1+a2+a3+a4+a5+a6=（f（x），f（x））
|a1+a2+a3+a4+a5+a6|=
| 2 |
|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=2(
| 2 |
| 6 |
| 2 |
所以：f(x)≤2(1+
| 2 |
| 3 |
当且仅当：
| ||
|
| ||
|
| ||
|
| ||
|
| ||
|
| ||
|
即sinx=0，即x=kπ时，函数f(x)≤2(1+
| 2 |
| 3 |
点评：本题考查的知识要点：巧妙利用三角函数的形式，利用基本不等式求解．
练习册系列答案
相关题目
函数f（x）=x+
+3在（-∞，0）上（ ）
| 4 |
| x |
| A、有最大值-1，无最小值 |
| B、无最大值，有最小值-1 |
| C、有最大值7，有最小值-1 |
| D、无最大值，有最小值7 |
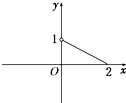已知定义在[-2，2]上的奇函数f（x）在（0，2]上的图象如图所示，