题目内容
A，B，C是平面内不共线的三点，点P在该平面内且有
+2
+3
=
，现将一粒芝麻随机撒在△ABC内，则这粒芝麻落在△PBC内的概率为（ ）
| PA |
| PB |
| PC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量加减混合运算及其几何意义,几何概型
专题：平面向量及应用,概率与统计
分析：先将已知向量式化为两个向量共线的形式，再利用平行四边形法则及向量数乘运算的几何意义，三角形面积公式确定面积之比，进而利用几何概型的概率公式即可得到结论．
解答：
解解答：：∵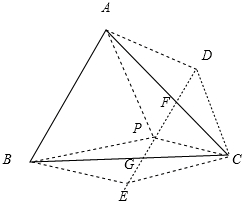
+2
+3
=
，
∴
+
+2（
+
）=
，
即
+
=-2（
+
），
分别取AC，BC的中点，F，G，
∵
+
=
=2
，
+
═
=2
，
∴
=2
，
∴F、P、G三点共线，且PF=2PG，GF为三角形ABC的中位线，
∴
=
=
=
=2，（h1，h2是相应三角形的高），
而S△APB=
S△ABC，
∴△APB，△APC，△BPC的面积之比等于3：2：1，
∴S△BPC：S△ABC=1：6，
∴由几何概型的概率公式可得将一粒芝麻随机撒在△ABC内，则这粒芝麻落在△PBC内的概率为
，
故选：D．
| PA |
| PB |
| PC |
| 0 |
∴
| PA |
| PC |
| PB |
| PC |
| 0 |
即
| PA |
| PC |
| PB |
| PC |
分别取AC，BC的中点，F，G，
∵
| PA |
| PC |
| PD |
| PF |
| PB |
| PC |
| PE |
| PG |
∴
| PF |
| PG |
∴F、P、G三点共线，且PF=2PG，GF为三角形ABC的中位线，
∴
| S△APC |
| S△BPC |
| ||
|
| h1 |
| h2 |
| PF |
| PG |
而S△APB=
| 1 |
| 2 |
∴△APB，△APC，△BPC的面积之比等于3：2：1，
∴S△BPC：S△ABC=1：6，
∴由几何概型的概率公式可得将一粒芝麻随机撒在△ABC内，则这粒芝麻落在△PBC内的概率为
| 1 |
| 6 |
故选：D．
点评：本题考查的知识点是几何概型的意义，关键是绘制满足条件的图形，数形结合找出满足条件的△PBC的面积大小与△ABC面积的大小之间的关系，再根据几何概型的计算公式进行求解．综合性较强，难度较大．
练习册系列答案
核心素养学练评系列答案
相关题目
已知函数f（x）=|lnx|，若
＞a＞b＞1，则f（a），f（b），f（c）比较大小关系正确的是（ ）
| 1 |
| c |
| A、f（c）＞f（b）＞f（a） |
| B、f（b）＞f（c）＞f（a） |
| C、f（c）＞f（a）＞f（b） |
| D、f（b）＞f（a）＞f（c） |
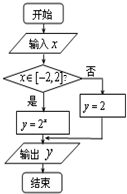
阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
甲、乙两个工人每人加工一个零件，加工为一等品的概率分别为
和
，两个零件是否被加工为一等品互相独立，则这两个工人加工的两个零件中至少有一个一等品的概率为（ ）
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A=（-1，2），集合B={x|-x2-2x+3＞0}，则A∪B=（ ）
| A、（-1，1） |
| B、（-3，2） |
| C、（-1，3） |
| D、（-1，2） |
一个算法的程序框图如图所示，若执行该程序输出的结果为| 99 |
| 100 |
| A、i≤98？ |
| B、i≤99？ |
| C、i≤100？ |
| D、i≤101？ |
阅读如图程序框图，输出的结果s的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|