题目内容
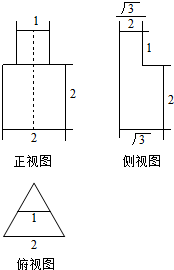
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知：该几何体是一个由四棱柱和三棱柱构成的组合体，分别求出两个棱柱的体积，相加可得答案．
解答：
解：由已知中的三视图可知：
该几何体是一个由四棱柱和三棱柱构成的组合体，
∵四棱柱底面是上底为1，下底为2，高为
的梯形，高为2，
故四棱柱体积为：
，
∵三棱柱底面是边长为1的正三角形，高为3，
故三棱柱体积为：
故组合体的体积V=
+
=
．
故选：D
该几何体是一个由四棱柱和三棱柱构成的组合体，
∵四棱柱底面是上底为1，下底为2，高为
| ||
| 2 |
故四棱柱体积为：
3
| ||
| 2 |
∵三棱柱底面是边长为1的正三角形，高为3，
故三棱柱体积为：
3
| ||
| 4 |
故组合体的体积V=
3
| ||
| 2 |
3
| ||
| 4 |
9
| ||
| 4 |
故选：D
点评：本题考查的知识点是由三视图求体积，其中根据已知分析出几何体的形状是解答的关键．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知数列{an}中，a1=1，an+1=2an+n-1，若利用如图所示的程序框图进行运算，则输出n的值为若函数f（x）=x2+x-a，则使得“函数y=f（x）在区间（-1，1）内有零点”成立的一个必要非充分条件是（ ）
A、-
| ||
B、-
| ||
| C、0＜a＜2 | ||
D、-
|
已知函数f（x）=|lnx|，若
＞a＞b＞1，则f（a），f（b），f（c）比较大小关系正确的是（ ）
| 1 |
| c |
| A、f（c）＞f（b）＞f（a） |
| B、f（b）＞f（c）＞f（a） |
| C、f（c）＞f（a）＞f（b） |
| D、f（b）＞f（a）＞f（c） |
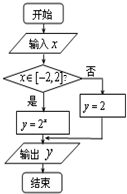
阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
阅读如图程序框图，输出的结果s的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|