题目内容
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=
(|x-a2|+|x-2a2|-3a2),若对于任意的实数x,都有f(x-1)≤f(x)成立,则实数a的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
考点:绝对值不等式的解法
专题:
分析:把x≥0时的f(x)改写成分段函数,求出其最小值,由函数的奇偶性可得x<0时的函数的最大值,由对?x∈R,都有f(x-1)≤f(x),可得2a2-(-4a2)≤1,求解该不等式得答案.
解答:
解:当x≥0时,
f(x)=
,
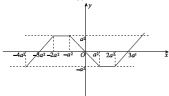
由f(x)=x-3a2,x>2a2,得f(x)>-a2;
当a2<x<2a2时,f(x)=-a2;
由f(x)=-x,0≤x≤a2,得f(x)≥-a2.
∴当x>0时,f(x)min=-a2.
∵函数f(x)为奇函数,
∴当x<0时,f(x)max=a2.
∵对?x∈R,都有f(x-1)≤f(x),
∴2a2-(-4a2)≤1,解得:-
≤a≤
.
故选:B.
f(x)=
|

由f(x)=x-3a2,x>2a2,得f(x)>-a2;
当a2<x<2a2时,f(x)=-a2;
由f(x)=-x,0≤x≤a2,得f(x)≥-a2.
∴当x>0时,f(x)min=-a2.
∵函数f(x)为奇函数,
∴当x<0时,f(x)max=a2.
∵对?x∈R,都有f(x-1)≤f(x),
∴2a2-(-4a2)≤1,解得:-
| ||
| 6 |
| ||
| 6 |
故选:B.
点评:本题考查了恒成立问题,考查了函数奇偶性的性质,运用了转化思想,对任意的实数x,都有f(x-1)≤f(x)成立的理解与应用是关键,也是难点,属于难题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知向量
=(2,-1),
=(3,x).若
•
=3,则x=( )
| a |
| b |
| a |
| b |
| A、6 | B、5 | C、4 | D、3 |
 如图,点O为正方体ABCD-A′B′C′D′的中心,点E为面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影不可能是( )
如图,点O为正方体ABCD-A′B′C′D′的中心,点E为面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影不可能是( )


