题目内容
下列等式成立的是( )
| A、{1,2,3}={2,1,3} |
| B、{(1,2)}={2,1} |
| C、{(1,2)}={(2,1)} |
| D、{(x,y)|x+y=1}={y|x+y=1} |
考点:集合的相等
专题:集合
分析:利用集合相等的定义:元素完全相同,与顺序无关,即可得出.
解答:
解:A.{1,2,3}={2,1,3},正确;
B.元素不相同;
C.元素不相同;
D.元素不相同.
故选:A.
B.元素不相同;
C.元素不相同;
D.元素不相同.
故选:A.
点评:本题考查了集合相等的定义:元素形式完全相同,与顺序无关,属于基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
已知函数y=f(x)是定义在R上的奇函数,且f(2+x)=f(2-x),则f(4)=( )
| A、4 | B、2 | C、0 | D、不确定 |
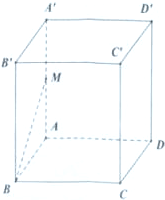 如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.
如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.