题目内容
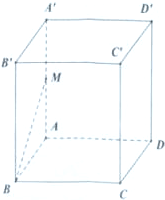 如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.
如图,在直平行六面体ABCD-A′B′C′D′中,底面ABCD是边长为2的菱形,∠ABC=60°,A′C与底面ABCD所成角的大小为arctan2,M为A′A的中点.(1)求四棱锥M-ABCD的体积;
(2)求异面直线BM与A′C所成角的大小(结果用反三角函数表示).
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:(1)连接AC,由底面ABCD是边长为2的菱形,∠ABC=60°,可得AC=2.由直平行六面体的性质可得∠A′CA是A′C与底面ABCD所成角,利用tan∠A′CA=
可得A′A=4.即可得出四棱锥M-ABCD的体积V=
•S菱形ABCD•EA.
(2)连接AC,BD,相交于点O,连接MO.则点O为AC的中点.利用三角形的中位线定理可得MO∥A′C.因此∠BMO或其补角为异面直线BM与A′C所成角.利用余弦定理可得:cos∠BMO=
即可得出.
| A′A |
| AC |
| 1 |
| 3 |
(2)连接AC,BD,相交于点O,连接MO.则点O为AC的中点.利用三角形的中位线定理可得MO∥A′C.因此∠BMO或其补角为异面直线BM与A′C所成角.利用余弦定理可得:cos∠BMO=
| BM2+OM2-BO2 |
| 2BM•OM |
解答:
解:(1)连接AC,
∵底面ABCD是边长为2的菱形,∠ABC=60°,
∴AC=2.∵直平行六面体ABCD-A′B′C′D′中,∴∠A′CA是A′C与底面ABCD所成角,
∵∠A′CA=arctan2,∴tan∠A′CA=
=2,∴A′A=4.
∵M为A′A的中点,∴MA=2.底面菱形ABCD的面积S=2×2×sin60°=2
.
∴四棱锥M-ABCD的体积V=
•S菱形ABCD•EA=
×2
×2=
.
(2)连接AC,BD,相交于点O,连接MO.
则点O为AC的中点.
又∵M为A′A的中点,∴MO∥A′C.
∴∠BMO或其补角为异面直线BM与A′C所成角.
在△BMO中,BO=
,MO=
=
,BM=
=2
.
由余弦定理可得:cos∠BMO=
=
.
∴异面直线BM与A′C所成角为arccos
.

∵底面ABCD是边长为2的菱形,∠ABC=60°,
∴AC=2.∵直平行六面体ABCD-A′B′C′D′中,∴∠A′CA是A′C与底面ABCD所成角,
∵∠A′CA=arctan2,∴tan∠A′CA=
| A′A |
| AC |
∵M为A′A的中点,∴MA=2.底面菱形ABCD的面积S=2×2×sin60°=2
| 3 |
∴四棱锥M-ABCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
(2)连接AC,BD,相交于点O,连接MO.
则点O为AC的中点.
又∵M为A′A的中点,∴MO∥A′C.
∴∠BMO或其补角为异面直线BM与A′C所成角.
在△BMO中,BO=
| 3 |
| AO2+AM2 |
| 5 |
| AB2+MA2 |
| 2 |
由余弦定理可得:cos∠BMO=
| BM2+OM2-BO2 |
| 2BM•OM |
| ||
| 4 |
∴异面直线BM与A′C所成角为arccos
| ||
| 4 |
点评:本题考查了直平行六面体的性质、菱形的性质、四棱锥的体积、异面直线所成的角、三角形的中位线定理、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
下列等式成立的是( )
| A、{1,2,3}={2,1,3} |
| B、{(1,2)}={2,1} |
| C、{(1,2)}={(2,1)} |
| D、{(x,y)|x+y=1}={y|x+y=1} |
已知等差数列{an}的前m项和为100,前3m项的和为-150,则它的前2m项的和为( )
| A、25 | B、-25 | C、50 | D、75 |
已知函数f(x)=2x-1,若f(a)=3,则a=( )
| A、5 | B、2 | C、1 | D、0 |
设x,y∈R,A={(x,y)|y=x},B={(x,y)|
=1},则A、B间的关系为( )
| y |
| x |
A、A
| ||
B、B
| ||
| C、A=B | ||
| D、A∩B=∅ |
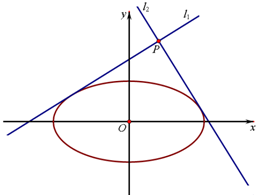 已知椭圆C:
已知椭圆C: