题目内容
已知锐角△ABC中，sinA=
，cosB=
，AB=8，则△ABC的面积为 ．
| 3 |
| 5 |
| 12 |
| 13 |
考点：解三角形,正弦定理
专题：解三角形
分析：过点C作AB的垂线，得到两个直角三角形，根据题意求出两直角三角形中AD，DB和CD的长，用三角形的面积公式求出三角形的面积．
解答：
解：如图：
过点C作AB的垂线，垂足为D．
∵sinA=
=
，
设CD=3x，AC=5x（x＞0）．AD=4x，
∵cosB=
，
可设CD=12y，CB=13y（y＞0），BD=5y．
∴3x=12y，5x+5y=8，
∴x=
．
则CD=3x=
．
故S△ABC=
AB•CD=
×8×
=
．
故答案是：
．
解：如图：过点C作AB的垂线，垂足为D．
∵sinA=
| 3 |
| 5 |
| CD |
| AC |
设CD=3x，AC=5x（x＞0）．AD=4x，
∵cosB=
| 12 |
| 13 |
可设CD=12y，CB=13y（y＞0），BD=5y．
∴3x=12y，5x+5y=8，
∴x=
| 32 |
| 25 |
则CD=3x=
| 96 |
| 25 |
故S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 96 |
| 25 |
| 384 |
| 25 |
故答案是：
| 384 |
| 25 |
点评：本题考查的是解直角三角形，过点C作AB的垂线得到两个直角三角形，由∠A的正弦和∠B的正切值，得到直角三角形中边的关系，求出AB和CD的长，用三角形的面积公式求出三角形的面积．
练习册系列答案
阅读快车系列答案
相关题目
以下四个关系：φ∈{0}，0∈φ，{φ}⊆{0}，φ
{0}，其中正确的个数是（ ）
| ? |
| ≠ |
| A、1 | B、2 | C、3 | D、4 |
下列等式成立的是（ ）
| A、{1，2，3}={2，1，3} |
| B、{（1，2）}={2，1} |
| C、{（1，2）}={（2，1）} |
| D、{（x，y）|x+y=1}={y|x+y=1} |
已知等差数列{an}的前m项和为100，前3m项的和为-150，则它的前2m项的和为（ ）
| A、25 | B、-25 | C、50 | D、75 |
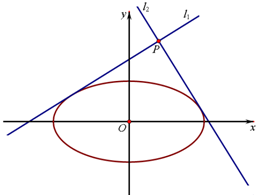已知椭圆C：