题目内容
10.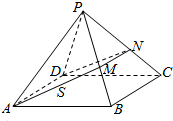 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )| A. | 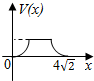 | B. | 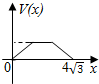 | C. | 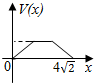 | D. | 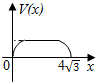 |
分析 根据棱锥的体积公式求出函数的解析式,并根据正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4$\sqrt{2}$,求出x的范围,判断函数的图象即可.
解答 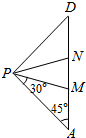 解:四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,
解:四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,
∴BC2=PB2+PC2-2PB•PCcos30°=16+16-2×4×4×$\frac{\sqrt{3}}{2}$=32-16$\sqrt{3}$,
∴底面正方形的面积s=32-16$\sqrt{3}$,h=xtan30°,
∴V(x)=$\frac{1}{3}$sh=$\frac{32-16\sqrt{3}}{3}$xtan30°,为线性函数,
∵四边形AMND的周长最小,正四棱锥侧面展开图如图所示,
∴正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4$\sqrt{2}$,
∴x≤4$\sqrt{2}$
故选:C.
点评 本题考查了函数解析式的求法,棱锥的体积公式,最短路线问题,属于中档题.

练习册系列答案
相关题目
1.如图是一个几何体的三视图,则在此几何体中,直角三角形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.在正方体ABCD-A1B1C1D1中,E,F分别为棱AB,BB1的中点,则直线BC1与EF所成角的余弦值是( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.过点(-1,0)与抛物线y=x2-1只有一个公共点的直线有( )
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
19.O为坐标原点,F为抛物线$C:y=\frac{1}{4}{x^2}$的焦点,P是抛物线C上一点,若|PF|=4,则△POF的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.
如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.