题目内容
1.如图是一个几何体的三视图,则在此几何体中,直角三角形的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由已知中的三视图,画出几何体的直观图,由勾股定理判断各个面的形状,可得答案.
解答 解:由已知中的三视图,可得几何体的直观图如下图所示:
由已知可得:棱锥的四个面均为直角三角形,
故选:D
点评 本题考查的知识点是简单几何体的三视图,几何体的直观图,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )| A. | $\frac{\sqrt{22}}{22}$ | B. | $\frac{\sqrt{22}}{11}$ | C. | $\frac{3\sqrt{22}}{22}$ | D. | $\frac{2\sqrt{22}}{11}$ |
16.在等差数列{an}中,a5=5,a10=15,则a15=( )
| A. | 20 | B. | 25 | C. | 45 | D. | 75 |
13.2015年春晚过后,为了研究演员上春晚次数与受关注的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(1)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$(精确到整数);
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
| 上春晚次数x(单位:次) | 1 | 2 | 4 | 6 | 8 |
| 粉丝数量y(单位:万人) | 5 | 10 | 20 | 40 | 80 |
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
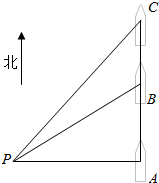 已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.
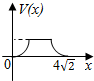
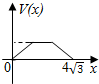
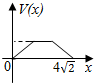
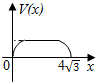
已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.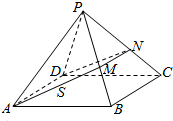 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )