题目内容
2.过点(-1,0)与抛物线y=x2-1只有一个公共点的直线有( )| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
分析 由题意可得(-1,0)在抛物线y=x2-1上,可得与抛物线只有一个公共点有两种情况:一种与对称轴平行;一种过(-1,0)与抛物线相切,即可得到所求条数.
解答 解:由(-1,0)在抛物线y=x2-1上,
可得与抛物线只有一个公共点的情况为:
当直线与对称轴平行,即为x=-1;
当直线和抛物线相切,由y=x2-1的导数为y′=2x,
可得切线的斜率为-2,切线的方程为y=-2(x+1).
综上可得,所求直线的条数为2.
故选:B.
点评 本题考查直线和抛物线的位置关系,注意讨论直线与对称轴的关系,属于基础题和易错题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则PA与平面PDE所成的角的正弦值为( )| A. | $\frac{\sqrt{22}}{22}$ | B. | $\frac{\sqrt{22}}{11}$ | C. | $\frac{3\sqrt{22}}{22}$ | D. | $\frac{2\sqrt{22}}{11}$ |
13.2015年春晚过后,为了研究演员上春晚次数与受关注的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(1)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$(精确到整数);
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
| 上春晚次数x(单位:次) | 1 | 2 | 4 | 6 | 8 |
| 粉丝数量y(单位:万人) | 5 | 10 | 20 | 40 | 80 |
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
17.下列说法正确的是( )
| A. | 动物和植物的机体都是细胞组成的;植物细胞中有细胞核,所以动物细胞中也有细胞核.此推理是归纳推理 | |
| B. | “由圆的性质推出球的有关性质”是类比推理 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 函数f(x)是可导函数,已知f′(a)=0则a为f(x)的极值点 |
14.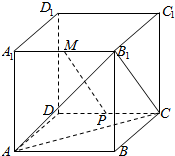 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{6}}]$ | B. | $[{\sqrt{6},2\sqrt{2}}]$ | C. | $[{\sqrt{6,}2\sqrt{3}}]$ | D. | $[{\sqrt{6,}3}]$ |
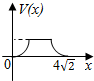
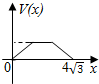
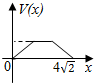
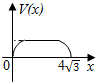
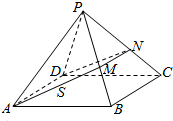 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )