题目内容
20．曲线y=$\frac{lnx}{x}$在点（1，0）处的切线是y=x-1．分析 欲求在点（1，0）处的切线的方程，只须求出其斜率即可，故先利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．
解答 解：∵y=$\frac{lnx}{x}$，
∴y′=$\frac{1-lnx}{{x}^{2}}$，
∴曲线y=$\frac{lnx}{x}$在点（1，0）处的切线的斜率为：k=1，
∴曲线y=$\frac{lnx}{x}$在点（1，0）处的切线的方程为：y=x-1，
故答案为：y=x-1．
点评 主要考查利用导数研究曲线上某点切线方程、直线方程的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
15．如图所示，角θ的终边与单位圆交于点P（-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{6}}{3}$），则cos（π-θ）的值为（ ）
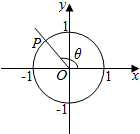
| A． | -$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
5．一个长方体的底面是边长为2的正方形，高为$\sqrt{2}$，其俯视图是面积为4的正方形，侧视图是一个面积为4的矩形，则该长方体正视图的面积为（ ）
| A． | 4 | B． | 2$\sqrt{2}$ | C． | 8 | D． | 4$\sqrt{2}$ |
12．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD是直角梯形，∠BAD=∠ADC=90°，E为CB的中点，AB=PA=AD=2CD，则PA与平面PDE所成的角的正弦值为（ ）
如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD是直角梯形，∠BAD=∠ADC=90°，E为CB的中点，AB=PA=AD=2CD，则PA与平面PDE所成的角的正弦值为（ ）| A． | $\frac{\sqrt{22}}{22}$ | B． | $\frac{\sqrt{22}}{11}$ | C． | $\frac{3\sqrt{22}}{22}$ | D． | $\frac{2\sqrt{22}}{11}$ |
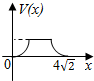
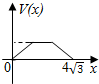
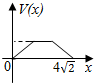
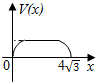
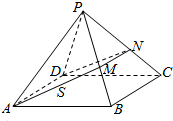在四棱锥P-ABCD中，各侧面是全等的等腰三角形，腰长为4且顶角为30°，底面是正方形（如图），在棱PB，PC上各有一点M、N，且四边形AMND的周长最小，点S从A出发依次沿四边形AM，MN，ND运动至点D，记点S行进的路程为x，棱锥S-ABCD的体积为V（x），则函数V（x）的图象是（ ）
