题目内容
18.在正方体ABCD-A1B1C1D1中,E,F分别为棱AB,BB1的中点,则直线BC1与EF所成角的余弦值是( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BC1与EF所成角的余弦值.
解答 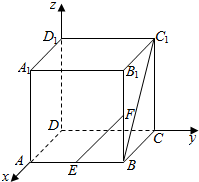 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则E(2,1,0),F(2,2,1),B(2,2,0),C1(0,2,2),
$\overrightarrow{B{C}_{1}}$=(-2,0,2),$\overrightarrow{EF}$=(0,1,1),
设直线BC1与EF所成角为θ,
则cosθ=|cos<$\overrightarrow{B{C}_{1}}$,$\overrightarrow{EF}$>|=$\frac{|\overrightarrow{B{C}_{1}}•\overrightarrow{EF}|}{|\overrightarrow{B{C}_{1}}|•|\overrightarrow{EF}|}$=$\frac{|2|}{\sqrt{8}•\sqrt{2}}$=$\frac{1}{2}$.
∴直线BC1与EF所成角的余弦值是$\frac{1}{2}$.
故选:B.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
13.2015年春晚过后,为了研究演员上春晚次数与受关注的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(1)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$(精确到整数);
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
| 上春晚次数x(单位:次) | 1 | 2 | 4 | 6 | 8 |
| 粉丝数量y(单位:万人) | 5 | 10 | 20 | 40 | 80 |
(2)试根据此方程预测该演员上春晚10次时的粉丝数;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
3.设α、β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | 若α⊥β,α∩β=n,m⊥n,则m⊥α | D. | 若α∩β=n,m∥α,m∥β,则m∥n |
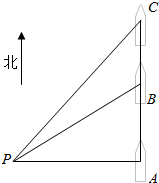 已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.
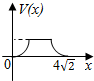
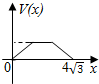
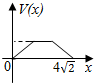
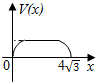
已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.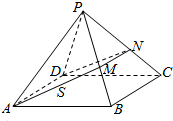 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )