题目内容
已知函数f(x)=ax2+ax+b(a>0),关于x的不等式f(x)≥c的解集为A.
(1)若f(1)=c=0,求集合A;
(2)若A=(-∞,m]∪[m+4,+∞),且f(x)的值域为[0,+∞),求
.
(1)若f(1)=c=0,求集合A;
(2)若A=(-∞,m]∪[m+4,+∞),且f(x)的值域为[0,+∞),求
| c |
| a |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)将1代入可得2a+b=0,进而可将不等式f(x)≥c可化为f(x)=a(x+2)(x-1)≥0,解得集合A;
(2)由A=(-∞,m]∪[m+4,+∞),且f(x)的值域为[0,+∞),可构造关于a,b,c的方程组,分类讨论可得
的值.
(2)由A=(-∞,m]∪[m+4,+∞),且f(x)的值域为[0,+∞),可构造关于a,b,c的方程组,分类讨论可得
| c |
| a |
解答:
解:(1)∵f(x)=ax2+ax+b,
∴f(1)=2a+b=c=0,
故不等式f(x)≥c可化为f(x)=a(x+2)(x-1)≥0,
又∵a>0,
∴A=(-∞,-2]∪[1,+∞)
(2)f(x)≥c化简得ax2+ax+b-c≥0,
若A=(-∞,m]∪[m+4,+∞),
则m和m+4是方程ax2+ax+b-c=0的两个根,
由韦达定理得,
m+m+4=-1,
解得:m=-
,
m•(m+4)=
=-
…(1),
由f(x)的值域是[0,+∞)得,
最小值
=0,即b(4a-b)=0…(2),
若b=0,则
=
,
若4a-b=0,
=
.
∴f(1)=2a+b=c=0,
故不等式f(x)≥c可化为f(x)=a(x+2)(x-1)≥0,
又∵a>0,
∴A=(-∞,-2]∪[1,+∞)
(2)f(x)≥c化简得ax2+ax+b-c≥0,
若A=(-∞,m]∪[m+4,+∞),
则m和m+4是方程ax2+ax+b-c=0的两个根,
由韦达定理得,
m+m+4=-1,
解得:m=-
| 5 |
| 2 |
m•(m+4)=
| b-c |
| a |
| 15 |
| 4 |
由f(x)的值域是[0,+∞)得,
最小值
| 4ab-b2 |
| 4a |
若b=0,则
| c |
| a |
| 15 |
| 4 |
若4a-b=0,
| c |
| a |
| 31 |
| 4 |
点评:本题考查的知识点是二次函数的性质,二次不等式的解法,难度不大,属于中档题.

练习册系列答案
相关题目
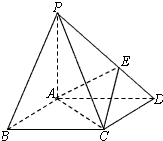 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD= 甲、乙两位学生参加数学竞赛培训,如图所示茎叶图的数据是他们在培训期间五次预赛的成绩.已知甲、乙两位学生的平均分相同.
甲、乙两位学生参加数学竞赛培训,如图所示茎叶图的数据是他们在培训期间五次预赛的成绩.已知甲、乙两位学生的平均分相同. 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a52=11.则a87=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a52=11.则a87=