题目内容
已知二次函数y=f(x)=x2+bx+c的图象过点(1,13),图象关于直线x=-
对称.
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,
①若函数y=g(x)-m的零点有三个,求实数m的取值范围;
②求函数g(x)在[t,2]上的最小值.
| 1 |
| 2 |
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,
①若函数y=g(x)-m的零点有三个,求实数m的取值范围;
②求函数g(x)在[t,2]上的最小值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由二次函数y=f(x)=x2+bx+c的图象过点(1,13),图象关于直线x=-
对称.构造关于b,c的方程,解方程,可得函数的解析式;
(2)求出函数g(x)=[f(x)-x2-13]•|x|的解析式,画出函数的图象,利用图象可分析出答案.
| 1 |
| 2 |
(2)求出函数g(x)=[f(x)-x2-13]•|x|的解析式,画出函数的图象,利用图象可分析出答案.
解答:
解:(1)二次函数y=f(x)=x2+bx+c的图象过点(1,13),图象关于直线x=-
对称.
∴
,
解得:
,
故y=f(x)=x2+x+11,
(2)由(1)得g(x)=[f(x)-x2-13]•|x|=(x-2)|x|,
其图象如下图所示:
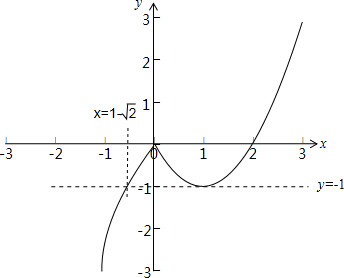
①若函数y=g(x)-m的零点有三个,即y=g(x)的图象与y=m有三个交点,
由图可得,m∈[-1,0]
②由图可得,
当t≤1-
时,函数g(x)在[t,2]上最小值为:g(t)=-t2+2t,
当1-
<t≤1时,函数g(x)在[t,2]上最小值为:g(1)=-1,
当1<t<2时,函数g(x)在[t,2]上最小值为:g(t)=t2-2t,
| 1 |
| 2 |
∴
|
解得:
|
故y=f(x)=x2+x+11,
(2)由(1)得g(x)=[f(x)-x2-13]•|x|=(x-2)|x|,
其图象如下图所示:
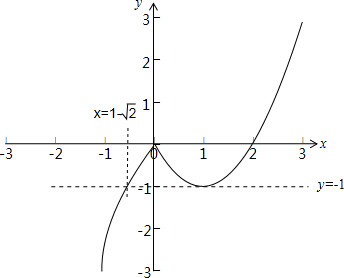
①若函数y=g(x)-m的零点有三个,即y=g(x)的图象与y=m有三个交点,
由图可得,m∈[-1,0]
②由图可得,
当t≤1-
| 2 |
当1-
| 2 |
当1<t<2时,函数g(x)在[t,2]上最小值为:g(t)=t2-2t,
点评:本题考查的知识点是二次函数的性质,二次不等式的解法,难度不大,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目