题目内容
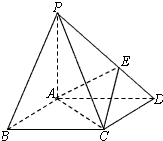 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=| 2 |
(Ⅰ)求二面角P-AC-E的大小;
(Ⅱ)试在棱PC上确定一点F,使得BF∥平面AEC.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明PA⊥平面ABCD,建立坐标系,求出平面ACE的一个法向量
=(1,-
,2
),平面ACP的一个法向量为
=(
,-
,0),利用向量的夹角公式,即可求二面角P-AC-E的大小;
(Ⅱ)取棱PC的中点F,线段PE的中点M,连接BD.设BD∩AC=O.连接BF,MF,BM,OE.结合菱形的性质及三角形中位线定理及面面平行的判定定理可得平面BMF∥平面AEC,进而由面面平行的性质得到BF∥平面AEC.
| n |
| 3 |
| 3 |
| m |
| ||
| 2 |
| 3 |
| 2 |
(Ⅱ)取棱PC的中点F,线段PE的中点M,连接BD.设BD∩AC=O.连接BF,MF,BM,OE.结合菱形的性质及三角形中位线定理及面面平行的判定定理可得平面BMF∥平面AEC,进而由面面平行的性质得到BF∥平面AEC.
解答:
解:(Ⅰ)∵底面ABCD是菱形,∠ABC=60°,
∴AB=AD=AC=1,
在△PAB中,由PA2+AB2=2=PB2,知PA⊥AB,
同理PA⊥AD
∴PA⊥平面ABCD.
建立坐标系,则A(0,0,0),B(
,-
,0),C(
,
,0),P(0,0,1),D(0,1,0),E(0,
,
),
∴
=(
,
,0),
=(0,
,
),
设平面ACE的一个法向量为
=(x,y,z),则
,
可取
=(1,-
,2
),
同理平面ACP的一个法向量为
=(
,-
,0),
∴cos<
,
>=
,
∴二面角P-AC-E的大小为60°;
(Ⅱ)存在点F为PC的中点,使BF∥平面AEC.
理由如下:
取棱PC的中点F,线段PE的中点M,连接BD.设BD∩AC=O.
连接BF,MF,BM,OE.
∵PE:ED=2:1,F为PC的中点,E是MD的中点,
∴MF∥EC,BM∥OE.
∵MF?平面AEC,CE?平面AEC,BM?平面AEC,OE?平面AEC,
∴MF∥平面AEC,BM∥平面AEC.
∵MF∩BM=M,
∴平面BMF∥平面AEC.
又BF?平面BMF,
∴BF∥平面AEC.
∴AB=AD=AC=1,
在△PAB中,由PA2+AB2=2=PB2,知PA⊥AB,
同理PA⊥AD
∴PA⊥平面ABCD.
建立坐标系,则A(0,0,0),B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∴
| AC |
| ||
| 2 |
| 1 |
| 2 |
| AE |
| 2 |
| 3 |
| 1 |
| 3 |
设平面ACE的一个法向量为
| n |
|
可取
| n |
| 3 |
| 3 |
同理平面ACP的一个法向量为
| m |
| ||
| 2 |
| 3 |
| 2 |
∴cos<
| n |
| m |
| 1 |
| 2 |
∴二面角P-AC-E的大小为60°;
(Ⅱ)存在点F为PC的中点,使BF∥平面AEC.
理由如下:
取棱PC的中点F,线段PE的中点M,连接BD.设BD∩AC=O.
连接BF,MF,BM,OE.
∵PE:ED=2:1,F为PC的中点,E是MD的中点,
∴MF∥EC,BM∥OE.
∵MF?平面AEC,CE?平面AEC,BM?平面AEC,OE?平面AEC,
∴MF∥平面AEC,BM∥平面AEC.
∵MF∩BM=M,
∴平面BMF∥平面AEC.
又BF?平面BMF,
∴BF∥平面AEC.
点评:本题考查的知识点是直线与平面平行的判定,用空间向量求平面间的夹角,(Ⅱ)的关键是证得平面BMF∥平面AEC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
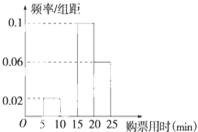 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).