题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在x=
时取得最大值4,在同一周期中,在x=
时取得最小值-4.
(1)求函数f(x)在[0,
]上的单调增区间;
(2)若f(
α+
)=2,α∈(0,π),求α的值.
| π |
| 12 |
| 5π |
| 12 |
(1)求函数f(x)在[0,
| 2π |
| 3 |
(2)若f(
| 2 |
| 3 |
| π |
| 12 |
考点:正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:(1)依题意可求得A=4,由周期T=
π可求得ω=3,3×
+φ=2kπ+
(k∈Z),0<φ<π可求得φ,从而可得函数f(x)的解析式;由2kπ-
≤3x+
≤2kπ+
(k∈Z),可求得函数f(x)在[0,
]上的单调增区间.
(2)由4sin[3(
α+
)+
]=4sin(2α+
)=4cos2α=2,可得cos2α=
,从而解得α的值.
| 2 |
| 3 |
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2π |
| 3 |
(2)由4sin[3(
| 2 |
| 3 |
| π |
| 12 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由题设知,A=4,
周期
=
-
=
,T=
π,又ω>0,
∴ω=
=3,
∴f(x)=4sin(3x+φ),
又x=
时,y取得最大值4,
∴3×
+φ=2kπ+
(k∈Z),
∴φ=2kπ+
(k∈Z),
∵0<φ<π,
∴φ=
.
∴f(x)=4sin(3x+
).
∵由2kπ-
≤3x+
≤2kπ+
(k∈Z),
得
kπ-
≤x≤
kπ+
(k∈Z),
∴函数f(x)在[0,
]上的单调增区间是:[0,
]∪[
,
].
(2)∵f(
α+
)=2,α∈(0,π),2α∈(0,2π),
∴4sin[3(
α+
)+
]=4sin(2α+
)=4cos2α=2,
∴cos2α=
,
∴2α=
或者
,
从而解得:α=
或
.
周期
| T |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| 2 |
| 3 |
∴ω=
| 2π | ||
|
∴f(x)=4sin(3x+φ),
又x=
| π |
| 12 |
∴3×
| π |
| 12 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 4 |
∵0<φ<π,
∴φ=
| π |
| 4 |
∴f(x)=4sin(3x+
| π |
| 4 |
∵由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
得
| 2 |
| 3 |
| π |
| 4 |
| 2 |
| 3 |
| π |
| 12 |
∴函数f(x)在[0,
| 2π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
| 3π |
| 4 |
(2)∵f(
| 2 |
| 3 |
| π |
| 12 |
∴4sin[3(
| 2 |
| 3 |
| π |
| 12 |
| π |
| 4 |
| π |
| 2 |
∴cos2α=
| 1 |
| 2 |
∴2α=
| π |
| 3 |
| 5π |
| 3 |
从而解得:α=
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查函数y=Asin(ωx+φ)的图象确定函数解析式,着重考查正弦函数的单调性与最值,属于中档题.

练习册系列答案
相关题目
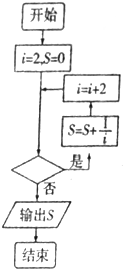 如图,给出的是计算
如图,给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2016 |
| A、i≤2021 |
| B、i≤2019 |
| C、i≤2017 |
| D、i≤2015 |
函数y=|sinx|的一个单调递增区间是( )
A、(
| ||
| B、(π,2π) | ||
C、(π,
| ||
| D、(0,π) |
斜率为3,在y轴上的截距为4的直线方程是( )
| A、3x-y+4=0 |
| B、x-3y-12=0 |
| C、3x-y-4=0 |
| D、3x-y-12=0 |
已知非空数集 A={x∈R|x2=a},则实数a的取值范围为( )
| A、a=0 | B、a>0 |
| C、a≠0 | D、a≥0 |