题目内容
若关于x的不等式ax2+2ax-4≥2x2+4x的解集为空集，则实数a的取值范围是（ ）
| A、（-2，2） |
| B、（-∞，2] |
| C、（-2，2] |
| D、（-∞，-2）∪（2，+∞） |
考点：一元二次不等式的应用
专题：计算题,不等式的解法及应用
分析：不等式ax2+2ax-4≥2x2+4x，可化为不等式（a-2）x2+（2a-4）x-4≥0，对二次项系数分为0和不为0两种情况讨论，在不为0时，把解集为空集转化为所对应图象均在x轴下方，列出满足的条件即可求实数a的取值范围．
解答：
解：不等式ax2+2ax-4≥2x2+4x，
可化为不等式（a-2）x2+（2a-4）x-4≥0
当a-2=0，-4≥0，符合要求；
当a-2≠0时，
∵关于x的不等式（a-2）x2+（2a-4）x-4≥0的解集为空集，
即所对应图象均在x轴下方，
故须
，
∴-2＜a＜2．
综上满足要求的实数a的取值范围是-2＜a≤2．
故选C．
可化为不等式（a-2）x2+（2a-4）x-4≥0
当a-2=0，-4≥0，符合要求；
当a-2≠0时，
∵关于x的不等式（a-2）x2+（2a-4）x-4≥0的解集为空集，
即所对应图象均在x轴下方，
故须
|
∴-2＜a＜2．
综上满足要求的实数a的取值范围是-2＜a≤2．
故选C．
点评：本题是对二次函数的图象所在位置的考查．其中涉及到对二次项系数的讨论，在作题过程中，只要二次项系数含参数，就要分情况讨论，这也是本题的一个易错点．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
抛物线y2=2px（p＞0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=90°．过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则
的最大值为（ ）
|
| ||
|
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点，则该椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
曲线y=
在点（0，0）处的切线方程为（ ）
| x |
| x+1 |
| A、y=-x | ||
B、y=
| ||
| C、y=x | ||
| D、y=2x |
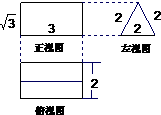已知某个几何体的三视图如图所示，试根据图中所标出的尺寸（单位：cm），可得这个几何体的表面积是（ ）A、18+
| ||
B、18+2
| ||
C、24+2
| ||
D、24+2
|
某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的体积为（ ）A、
| ||||
| B、π | ||||
C、
| ||||
D、
|