题目内容
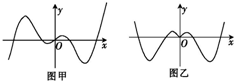已知图甲为函数y=f（x）的图象，则图乙中的图象对应的函数可能为（ ）| A、y=|f（x）| |
| B、y=f（|x|） |
| C、y=f（-|x|） |
| D、y=-f（-|x|） |
考点：函数的图象
专题：函数的性质及应用
分析：由图乙可以知道，该函数为偶函数，且x＞0时，函数图象与原函数图象相同，左边图象与右边对称，只有y=f（|x|）符合要求．
解答：
解：比较图甲与图乙中两个函数的图象，x＞0时，函数图象与原函数图象相同，只有B符合，
观察图乙中函数的图象，图象关于y轴对称，故图乙中的图象对应的函数为偶函数，选项B仍符合，
故选：B．
观察图乙中函数的图象，图象关于y轴对称，故图乙中的图象对应的函数为偶函数，选项B仍符合，
故选：B．
点评：本题只有考查函数的图象，研究函数的图象应从函数的性质入手，特别是函数的奇偶性、对称性．
练习册系列答案
轻松暑假总复习系列答案
相关题目
若函数f（x）=x2-2（1-a2）x-a在区间（1，3）内有零点，则实数a的取值范围是（ ）
A、（0，
| ||
B、（-1，-
| ||
| C、（-1，1） | ||
D、（-
|
某产品的广告费用x与销售额y的统计数据如表：
根据表中可得线性回归方程
=
x+
中的
为9.4，据此模型预报广告费用为7万元时销售额为（ ）
| 广告费用x（万元） | 2 | 3 | 4 | 5 |
| 销售额y（万元） | 26 | 39 | 49 | 54 |
| y |
| b |
| a |
| b |
| A、73.6万元 |
| B、73.8万元 |
| C、74.9万元 |
| D、75.1万元 |