题目内容

求函数f（x）=2lnx-ax单调区间．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：先求出函数的定义域，求出函数f（x）的导函数，在定义域下令导函数大于0得到函数的递增区间．即可求出单调减区间．
解答： 解：∵函数f（x）=2lnx-ax的定义域为（0，+∞），
则f′（x）=
2
x
-a，
当a＞0时，则f′（x）＞0，解得0＜x＜
2
a
．函数的增区间为：（0，
2
a
），单调减区间为（
2
a
，+∞）．
当a≤0时，f′（x）＞0恒成立，函数的单调增区间为（0，+∞）．
点评：求函数的单调区间，应该先求出函数的导函数，令导函数大于0得到函数的递增区间，令导函数小于0得到函数的递减区间．注意参变量的讨论．
练习册系列答案
相关题目
已知双曲线3x2-y2+3=0与坐标轴的上下交点为B，A，动点P满足|
PA
|+|
PB
|=4．求动点P的轨迹E的方程．
已知2
a
+
b
=（0，-3，-10），
c
=（1，-2，-2），
a
•
c
=4，|
b
|=12，则＜
b
，
c
＞=
 
．
如图，点P从点O出发，按逆时针方向沿周长为l的圆运动一周，设O，P两点连线的距离为y，点P走过的路程为x，当0＜x＜
l
2
时，y关于x的函数解析式为
 
．
已知函数f（x）=
2
cos(x-
π
12
)，x∈R．求f（-
π
6
）的值．
如图所示，已知△OFQ的面积为S，且
OF
•
FQ
=1，设|
OF
|=c，S=
14
4
c，若以O为中心，F为焦点的双曲线经过点Q，建立适当的直角坐标系，求|
OQ
|最小时此双曲线的方程．
已知函数f（x）=
log3x，x＞0
2x，x≤0

（Ⅰ）求f（f（
1
9
））的值；
（Ⅱ）若f（a）=
1
4
，求实数a的值；
（Ⅲ）求不等式f（x+1）＞
1
2
的解集．
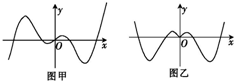已知图甲为函数y=f（x）的图象，则图乙中的图象对应的函数可能为（　　）
A、y=|f（x）|
B、y=f（|x|）
C、y=f（-|x|）
D、y=-f（-|x|）
在2点至3点之间的某一时刻，分针与时针分别在钟面上“2”字的两侧，而且与“2”字的距离相等，这一时刻是（　　）
A、2时6
3
13
分
B、2时7
1
13
分
C、2时8
5
13
分
D、2时9
3
13
分

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网