题目内容
数列{an}中,a1=1,其前n项和满足
=an(Sn-
).
(1)求Sn的表达式;
(2)设bn=
,数列{bn}的前n项和为Tn,求Tn.
| S | 2 n |
| 1 |
| 2 |
(1)求Sn的表达式;
(2)设bn=
| Sn |
| 2n+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)把an=Sn-Sn-1代入
=an(Sn-
),整理得
-
=2.由此可知数列{
}是公差为2的等差数列,求得其通项公式后得Sn的表达式;
(2)把Sn代入bn=
,然后利用裂项相消法求和.
| S | 2 n |
| 1 |
| 2 |
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| Sn |
(2)把Sn代入bn=
| Sn |
| 2n+1 |
解答:
解:(1)由
=an(Sn-
)(n≥2),得
Sn+12=(Sn-Sn-1)(Sn-
)=Sn2-
Sn-SnSn-1+
Sn-1,
∴Sn-1-Sn=2SnSn-1,
∴
-
=2.
即数列{
}是公差为2的等差数列,
又
=
=1,
∴
=1+2(n-1)=2n-1,
则Sn=
;
(2)bn=
=
=
(
-
),
∴Tn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.
| S | 2 n |
| 1 |
| 2 |
Sn+12=(Sn-Sn-1)(Sn-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn-1-Sn=2SnSn-1,
∴
| 1 |
| Sn |
| 1 |
| Sn-1 |
即数列{
| 1 |
| Sn |
又
| 1 |
| S1 |
| 1 |
| a1 |
∴
| 1 |
| Sn |
则Sn=
| 1 |
| 2n-1 |
(2)bn=
| Sn |
| 2n+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查了数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
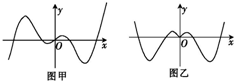 已知图甲为函数y=f(x)的图象,则图乙中的图象对应的函数可能为( )
已知图甲为函数y=f(x)的图象,则图乙中的图象对应的函数可能为( )| A、y=|f(x)| |
| B、y=f(|x|) |
| C、y=f(-|x|) |
| D、y=-f(-|x|) |
定义max{a,b}=
,设实数x,y满足约束条件
,且z=max{3x+y,2x-y},则z的取值范围为( )
|
|
A、[-
| ||
| B、[-4,6] | ||
| C、[-8,7] | ||
| D、[-4,7] |
某班学生体检中检查视力的结果如表,从表中可以看出,全班视力数据的众数是( )
| 视力 | 0.5以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 占全班人数百分比 | 2% | 6% | 3% | 20% | 65% | 4% |
| A、0.9 | B、1.0 |
| C、20% | D、65% |
在2点至3点之间的某一时刻,分针与时针分别在钟面上“2”字的两侧,而且与“2”字的距离相等,这一时刻是( )
A、2时6
| ||
B、2时7
| ||
C、2时8
| ||
D、2时9
|
 如图,点P从点O出发,按逆时针方向沿周长为l的圆运动一周,设O,P两点连线的距离为y,点P走过的路程为x,当0<x<
如图,点P从点O出发,按逆时针方向沿周长为l的圆运动一周,设O,P两点连线的距离为y,点P走过的路程为x,当0<x<