题目内容
(1)解不等式:5(x+2)2≥1-2(x-1);
(2)已知a<1,解关于x的不等式
>1.
(2)已知a<1,解关于x的不等式
| ax |
| x-2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:(1)移项分解因式可把原不等式可化(x+1)(5x+17)≥0,易得解集;
(2)原不等式可化为
>0,由于a<1,原不等式可化为
<0,分类讨论可得.
(2)原不等式可化为
| (a-1)x+2 |
| x-2 |
x-
| ||
| x-2 |
解答:
解:(1)原不等式可化为5(x+2)2-1+2(x-1)≥0,
整理可得5x2+22x+17≥0,分解因式可得(x+1)(5x+17)≥0,
∴不等式的解集为:{x|x≤-
或x≥-1}
(2)原不等式可化为
>0.
∵a<1,∴a-1<0,则原不等式可化为
<0,
故当0<a<1时,2<
,原不等式的解集为{x|2<x<
};
当a=0时,原不等式的解集为∅;
当a<0时,2>
,原不等式的解集为{x|
<x<2}
整理可得5x2+22x+17≥0,分解因式可得(x+1)(5x+17)≥0,
∴不等式的解集为:{x|x≤-
| 17 |
| 5 |
(2)原不等式可化为
| (a-1)x+2 |
| x-2 |
∵a<1,∴a-1<0,则原不等式可化为
x-
| ||
| x-2 |
故当0<a<1时,2<
| 2 |
| 1-a |
| 2 |
| 1-a |
当a=0时,原不等式的解集为∅;
当a<0时,2>
| 2 |
| 1-a |
| 2 |
| 1-a |
点评:本题考查不等式的解集,涉及分类讨论的思想,属基础题.

练习册系列答案
相关题目
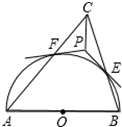 如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.
如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB. 如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.
如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.