题目内容

证明：若g（x）=x2+ax+b，则g（
x1+x2
2
）≤
g(x1)+g(x2)
2
．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据g（x），分别求出g(
x1+x2
2
)，
g(x1)+g(x2)
2
进行作差即可．
解答： 证明：g(
x1+x2
2
)-
g(x1)+g(x2)
2
=(
x1+x2
2
)2+
a
2
(x1+x2)+b-
x12+ax1+b+x22+ax2+b
2
=(
x1+x2
2
)2-
x12+x22
2
=
-x12-x22+2x1x2
4
=
-(x1-x2)2
4
≤0；
∴g(
x1+x2
2
)≤
g(x1)+g(x2)
2
．
点评：考查根据函数解析式求函数值，利用作差法证明不等式．
练习册系列答案
相关题目
先化简：（a-
-2a-1
a
）÷
1-a2
a2-a
，再给a选择一个合适的数代入求值．
某苗木公司要为一小区种植三棵景观树，有甲、乙两种方案．
甲方案：若第一年种植后全部成活，小区全额付款8千元；若第一年成活率不足
1
2
，终止合作，小区不付任何款项；若成活率超过
1
2
，但没有全成活，第二年公司将对没有成活的树补种，若补种的树全部成活，小区付款8千元，否则终止合作，小区付给公司2千元．
乙方案：只种树不保证成活，每棵树小区付给公司1.3千元．苗木公司种植每棵树的成本为1千元，这种树的成活率为
2
3
．
（Ⅰ）若实行甲方案，求小区给苗木公司付款的概率；
（Ⅱ）公司从获得更大利润考虑，应选择那种方案．
将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，记第一次出现的点数为a，第二次出现的点数为b．设复数z=a+bi．
（1）求事件“z-3i为实数”的概率；
（2）求事件“|Z-2|≤3”有多少种不同的情况，并加以说明．
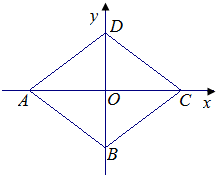如图，在平面直角坐标系中，菱形ABCD的两个顶点C，D的坐标分别为（4，0），（0，3）．现有两动点P，Q分别从A，C同时出发，点P沿线段AD以每秒1个单位的速度向终点D运动，点Q沿折线CBA以每秒2个单位的速度向终点A运动，设运动时间为t秒．
（1）填空：菱形ABCD的边长是
 
，面积是
 
；
（2）探究下列问题：
①当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，并求出S的最大值；
②在点P和点Q的运动过程中，△APQ能否成为等腰三角形，若能，请直接写出t的值，若不能，请说明理由．
（1）解不等式：5（x+2）2≥1-2（x-1）；
（2）已知a＜1，解关于x的不等式
ax
x-2
＞1．
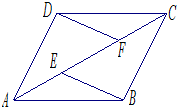如图，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF，AD=DC求证：四边形ABCD是菱形．
已知函数f（x）=lnx+ax-a2x2（a∈R）．
（1）求f（x）的单调区间与极值．
（2）若函数f（x）在区间（1，+∞）上是单调递减函数，求实数a的取值范围．
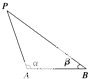外国船只除特许外，不得进入离我国海岸线d海里以内的区域，如图所示，设A与B是我们的观测站，A与B的距离为s海里，海岸线是过A、B的直线，一外国船只在P点，在A站测得∠BAP=α，同时在B站测得∠ABP=β，则α与β满足三角不等式为
 
时，就应当向此未经特许的外国船只发出警告，命令其退出我国海域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网