题目内容
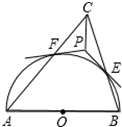 如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.
如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.考点:与圆有关的比例线段
专题:立体几何
分析:连接AE、BF得交点Q,由已知得CQ⊥AB.延长FP到点K,使PK=PF,连接EF、KE.则∠PEF=∠PFE=∠EAF.连接PQ并延长交AB于点H,由已知推导出K、F、Q、E四点共圆,由此能证明CP⊥AB.
解答:
证明:如图,连接AE、BF得交点Q,
∵∠AEB=∠AFB=90°,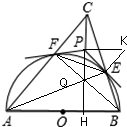
∴点Q为△ABC的垂心,
∴CQ⊥AB.①
延长FP到点K,使PK=PF,连接EF、KE.
由题意知∠PEF=∠PFE=∠EAF.
连接PQ并延长交AB于点H,
∵∠EQF=180°-∠AQF
=180°-(90°-∠EAF)=90°+∠EAF=90°+∠PEF,
∠K=
∠EPF=90°-∠PEF
∴∠EQF+∠K=180°.
故K、F、Q、E四点共圆,
∵PK=PE=PF,
∴P必是该圆的圆心.
∴PQ=PF.
∴∠PQF=∠PFQ=∠PFB=∠FAB=∠FAH,
∴A、H、Q、F四点共圆.
则∠PHA=∠QHA=180°-∠QFA=90°,
∴PH⊥AB,即PQ⊥AB.②
由①、②知,C、P、Q三点共线,
∴CP⊥AB.
∵∠AEB=∠AFB=90°,

∴点Q为△ABC的垂心,
∴CQ⊥AB.①
延长FP到点K,使PK=PF,连接EF、KE.
由题意知∠PEF=∠PFE=∠EAF.
连接PQ并延长交AB于点H,
∵∠EQF=180°-∠AQF
=180°-(90°-∠EAF)=90°+∠EAF=90°+∠PEF,
∠K=
| 1 |
| 2 |
∴∠EQF+∠K=180°.
故K、F、Q、E四点共圆,
∵PK=PE=PF,
∴P必是该圆的圆心.
∴PQ=PF.
∴∠PQF=∠PFQ=∠PFB=∠FAB=∠FAH,
∴A、H、Q、F四点共圆.
则∠PHA=∠QHA=180°-∠QFA=90°,
∴PH⊥AB,即PQ⊥AB.②
由①、②知,C、P、Q三点共线,
∴CP⊥AB.
点评:本题考查两直线垂直的证明,解题时要注意四点共圆的性质的合理运用,是中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
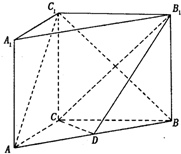 如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点.
如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点.