题目内容
 如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.
如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.(Ⅰ)求异面直线OC与MD所成角的正切值;
(Ⅱ)求点M到平面OCD的距离.
考点:异面直线及其所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(I)如图所示,设线段AC的中点为E,连接ME.利用三角形的中位线定理可得:ME∥OC,因此∠EMD或其补角为异面直线OC与MD所成角.利用勾股定理的逆定理可得∠MED=90°.利用tan∠EMD=
即可得出.
(II)作MF⊥OD于F,利用正方体的性质、线面垂直的判定定理可得CD⊥平面ADO.即可得到MF⊥平面OCD.
| DE |
| EM |
(II)作MF⊥OD于F,利用正方体的性质、线面垂直的判定定理可得CD⊥平面ADO.即可得到MF⊥平面OCD.
解答:
解:(I)如图所示,设线段AC的中点为E,连接ME.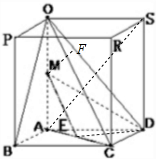
则ME∥OC,
∴∠EMD或其补角为异面直线OC与MD所成角.
DE=
,EM=
OC=
,MD=
,
∵(
)2+(
)2=(
)2,
∴∠MED=90°.
∴tan∠EMD=
=
=
.
(Ⅱ)作MF⊥OD于F,
∵CD⊥平面ADO.
∴CD⊥MF.
∴MF⊥平面OCD.
∴点M到平面OCD的距离MF=
AS=
×2
=
.

则ME∥OC,
∴∠EMD或其补角为异面直线OC与MD所成角.
DE=
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
∵(
| 2 |
| 3 |
| 5 |
∴∠MED=90°.
∴tan∠EMD=
| DE |
| EM |
| ||
|
| ||
| 3 |
(Ⅱ)作MF⊥OD于F,
∵CD⊥平面ADO.
∴CD⊥MF.
∴MF⊥平面OCD.
∴点M到平面OCD的距离MF=
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| ||
| 2 |
点评:本题考查了正方体的性质、异面直线所成的角、三角形的中位线定理、勾股定理的逆定理、线面垂直的判定与性质定理、点到平面的距离,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
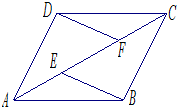 如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.
如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.