题目内容
袋中有三个白球，两个黑球，现每次摸出一个球，不放回的摸取两次，则在第一次摸到黑球的条件下，第二次摸到白球的概率为 ．
考点：条件概率与独立事件
专题：计算题,概率与统计
分析：本题条件概率，需要做出第一次取到黑球的概率和第一次取到黑球、第二次取到白球的概率，根据条件概率的公式，代入数据得到结果．
解答：
解：记事件A为“第一次取到黑球”，事件B为“第二次取到白球”，
则事件AB为“第一次取到黑球、第二次取到白球”，
依题意知P（A）=
，P（AB）=
×
，
∴在第一次取到黑球的条件下，第二次取到白球的概率是P（B|A）=
．
故答案为：
．
则事件AB为“第一次取到黑球、第二次取到白球”，
依题意知P（A）=
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 4 |
∴在第一次取到黑球的条件下，第二次取到白球的概率是P（B|A）=
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查概率的计算，考查学生分析解决问题的能力，比较基础．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
若数列{an}满足
-
=0，n∈N*，p为非零常数，则称数列{an}为“梦想数列”．已知正项数列{
}为“梦想数列”，且b1b2b3…b99=299，则b8+b92的最小值是（ ）
| 1 |
| an+1 |
| p |
| an |
| 1 |
| bn |
| A、2 | B、4 | C、6 | D、8 |
若F（5，0）是双曲线
-
=1（m是常数）的一个焦点，则m的值为（ ）
| x2 |
| 16 |
| y2 |
| m |
| A、3 | B、5 | C、7 | D、9 |
设函数f（x）=
+a是奇函数（a为常数），则f（x）＜0的解集为（ ）
| 1 |
| 2x+1 |
| A、（0，+∞） | ||
| B、（1，+∞） | ||
| C、（-1，0）∪（0，1） | ||
D、（
|
在△ABC中，BC=7，AB=5，∠A=120°，则△ABC的面积等于（ ）
A、5
| ||||
B、10
| ||||
C、
| ||||
D、
|
设{an}是等差数列，{bn}是等比数列，Sn、Tn分别是数列{an}、{bn}的前n项和．若a3=b3，a4=b4，且
=7，则
的值为（ ）
| S5-S3 |
| T4-T2 |
| a5 |
| b3+b6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果b＜a＜0，那么下列不等式错误的是（ ）
| A、c+b＜c+a | ||||
| B、a2＜b2 | ||||
| C、bc2＜ac2 | ||||
D、
|
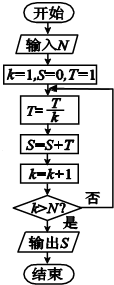阅读如图的程序框图，解答以下问题：| C | 2 6 |
| A、4 | B、8 | C、10 | D、15 |