Question

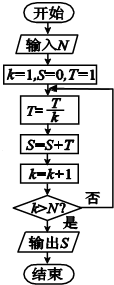阅读如图的程序框图，解答以下问题：
（1）如果输入的N=3，那么输出的S为多少？
（2）对于输入的任何正整数N，都有对应S输出．证明：S＜2．

Answer 1

考点：程序框图

专题：算法和程序框图

分析：（1）写出各次循环得到的结果，直到满足判断框中的条件，退出循环；
（2）由框图判定出S=1+

1

2!

+

1

3!

=

5

3

，根据n＞2时有n＞2时有n!＞2^n-1，得证．

解答： 解：（1）第一次循环得到：T=1，S=1，k=2；
第二次循环得到：T=

1

2

，S=1+

1

2

，k=3；
T=

1

2×3

，S=1+

1

2

+

1

2×3

，k=4，
4＞3满足条件，
输出S=1+

1

2!

+

1

3!

=

5

3

（2）由题意知S=1+

1

2!

+

1

3!

+…+

1

n!

，
而n＞2时有n!＞2^n-1
∴n＞2，S＜1+

1

2

+

1

22

+…+

1

2n-1

=2-(

1

2

)n-1＜2
经验证，n=1，2也有S＜2．

点评：本题考查的知识点是循环结构，在求程序的运行结果时，我们常使用模拟运行的方法，如何管理程序运行过程中各变量的值，是解答本题的关键