题目内容
2.若$\frac{1+cosα}{sinα}$=2,则cosα-3sinα=( )| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
分析 首先将已知等式利用倍角公式化为$\frac{α}{2}$三角函数式,求出tan$\frac{α}{2}$,对所求变形为$\frac{α}{2}$的齐次代数式求值.
解答 解:由已知等式得到$\frac{2co{s}^{2}\frac{α}{2}}{2sin\frac{α}{2}cos\frac{α}{2}}=\frac{cos\frac{α}{2}}{sin\frac{α}{2}}=2$,所以tan$\frac{α}{2}$=$\frac{1}{2}$,
cosα-3sinα=$\frac{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}-6sin\frac{α}{2}cos\frac{α}{2}}{si{n}^{2}\frac{α}{2}+co{s}^{2}\frac{α}{2}}$
=$\frac{1-ta{n}^{2}\frac{α}{2}-6tan\frac{α}{2}}{ta{n}^{2}\frac{α}{2}+1}$
=$\frac{1-\frac{1}{4}-3}{\frac{1}{4}+1}=-\frac{9}{5}$;
故选C.
点评 本题考查了三角函数式的化简求值;正确利用倍角公式对已知等式变形,将所求化为齐次代数式是关键.

练习册系列答案
相关题目
10.已知点M(x,y)是圆C:x2+y2-2x=0的内部任意一点,则点M满足y≥x的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{1}{2π}$ | D. | $\frac{π-2}{4π}$ |
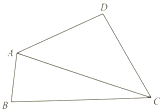 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.