题目内容
8. 某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )| A. | 3 | B. | 4 | C. | 9 | D. | 6 |
分析 由已知中的三视图,可得该几何体是一个以俯视图为底面的四棱锥,高为x,根据已知中棱锥的体积构造方程,解方程,可得答案.
解答 解:由已知中的三视图,可得该几何体是一个以俯视图为底面的四棱锥,高为x,
棱锥的底面是上底长2,下底长4,高为4的梯形,
故S=$\frac{1}{2}$×(2+4)×4=12,
又由该几何体的体积是12,
∴12=$\frac{1}{3}$×12x,
即x=3,
故选:A.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
3.双曲线$\frac{y^2}{3}-{x^2}=1$的焦点坐标是( )
| A. | $(±\sqrt{2},0)$ | B. | $(0,±\sqrt{2})$ | C. | (0,±2) | D. | (±2,0) |
20.已知向量$\overrightarrow{a}$=(0,1,1),$\overrightarrow{b}$=(1,2,0),则同时与$\overrightarrow{a}$,$\overrightarrow{b}$垂直的单位向量$\overrightarrow{e}$=( )
| A. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$ | B. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | ||
| C. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | D. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ |
17.已知x=log52,y=ln2,z=${2}^{\frac{1}{2}}$,则下列结论正确的是( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
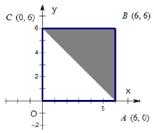 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).