题目内容
16.在直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}\right.$(α为参数,-π<α<0),曲线C2的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}-\frac{\sqrt{3}}{2}t}\\{y=5+\sqrt{3}t}\end{array}\right.$(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=-$\frac{π}{4}$与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
分析 (1)利用三种方程的转化方法,求曲线C1的极坐标方程和曲线C2的普通方程;
(2)通过方程组求出P、Q坐标,然后利用两点间距离公式求解即可.
解答 解:(1)曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}\right.$(α为参数,-π<α<0),
普通方程为(x-1)2+y2=1,(y<0),
极坐标方程为ρ=2cosθ,θ∈(-$\frac{π}{2}$,0),曲线C2的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}-\frac{\sqrt{3}}{2}t}\\{y=5+\sqrt{3}t}\end{array}\right.$(t为参数),
普通方程2x+y-6=0;
(2)θ=-$\frac{π}{4}$,$ρ=\sqrt{2}$,即P($\sqrt{2}$,-$\frac{π}{4}$);
θ=-$\frac{π}{4}$代入曲线C2的极坐标方程,可得ρ′=6$\sqrt{2}$,即Q(6$\sqrt{2}$,-$\frac{π}{4}$),
∴|PQ|=6$\sqrt{2}$-$\sqrt{2}$=5$\sqrt{2}$.
点评 本题考查极坐标与参数方程的应用,化为普通方程的方法,两点间距离公式的应用,考查计算能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7.已知函数$f(x)=xcosx-\frac{a}{x}sinx-sinx,x∈({-kπ,0})∪({0,kπ})$(其中k为正整数,a∈R,a≠0),则f(x)的零点个数为( )
| A. | 2k-2 | B. | 2k | C. | 2k-1 | D. | 与a有关 |
4.已知集合A={1,2,3},B={x∈Z|(x+2)(x-3)<0},则A∪B( )
| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
11.设抛物线K:x2=2py(p>0),焦点为F,P是K上一点,K在点P处的切线为l,d为F到l的距离,则( )
| A. | $\frac{d}{|PF|}$=p | B. | $\frac{d}{|PF{|}^{2}}$=p | C. | $\frac{d}{|PF|}$=2p | D. | $\frac{{d}^{2}}{|PF|}$=$\frac{p}{2}$ |
8. 某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
 某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是12,则正视图中的x的值是( )| A. | 3 | B. | 4 | C. | 9 | D. | 6 |
5.已知不等式x2-ax+a-2>0的解集为(-∞,x1)∪(x2+∞),其中x1<0<x2,则${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | 2 | D. | $-\frac{3}{2}$ |
6.已知某几何体的三视图及相关数据如图所示,则该几何体的体积为( )
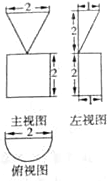

| A. | 2π | B. | $\frac{8}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{π}{3}$+4 |